and
and the angle q spanned by them.
Scalar product in two dimensions
(a) Geometric definition
Figure 4 below shows two vectors and
and the angle q spanned by them.
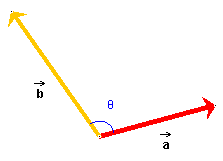
Figure 4
The scalar product 
is equal to
= ab cos q.
(4)
Comment. For q = 0, the two vectors
point in the same direction and Eq.(4) reduces to = ab, since cos 0 = 1. This is Eq.(1)
on Page 1. Thus, the scalar product in one dimension is a special
case of that in two dimensions. Check that this is true also for
q = 180o when the two vectors
are oppositely directed.
(b) Analytic definition
Figure 5 below shows two vectors and
and their scalar components
(ax,ay) and
(bx,by) relative to a pair of
Cartesian (right-angle) x and y axes.
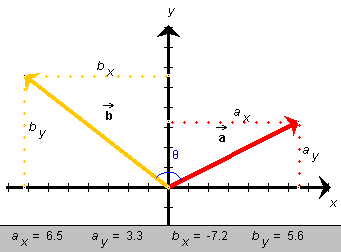
Figure 5
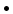
The scalar product is equal to
=
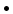
axbx +
ayby .(5)
Comment 1. If both vectors are parallel to the x-axis,
their y-components are zero and Expression (5) for the scalar
product reduces to =
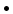
axbx, which is Eq.(3) from Page 1.
Again we see that the scalar product in one dimension is a special
case of that in two dimensions.
Comment 2. The scalar product is a geometric quantity that depends only on the two vectors involved, not on the axes used to define the scalar components. Thus, if the axes in Figure 5 are rotated, the values of (ax,ay) and (bx,by) will change, but not that of the combination on the right-hand side of Eq.(5). This equation does, however, assume that the x and y axes are perpendicular to each other, i.e., that the coordinates are Cartesian.
Scalar product in three dimensions
(a) Geometric definition
The definition is exactly the same as in two dimensions, as given by Eq.(4) above.
(b) Analytic definition
Eq.(5) must be modified to include also the term azbz. Thus,
=
axbx +
ayby +
azbz.(6)