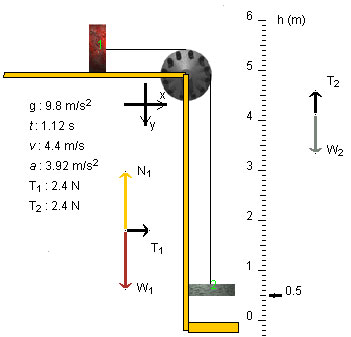
Yes, the tension in the string is equal to 2.35 N. The snapshot above shows the system at an instant when it is in motion.

Solution

Plan It. Apply Newton's second law to the two blocks separately. This will give two equations for two unknowns: the tension T and the magnitude a of the acceleration of the blocks. (Both blocks will have accelerations of the same magnitude because the string is assumed to not stretch.) Note that the magnitudes T₁ and T₂ of the forces exerted by the string on blocks 1 and 2, respectively, are equal to the tension T: T = T₁ = T₂. The two equations for T and a can be solved.

Setup

• The coordinate axes are defined as in the snapshot: x horizontal and to the right, y vertical and downward.
• The free-body diagrams for the two blocks are shown in the snapshot.
• Applying Newton's second law to the two blocks separately yields the following two equations:

     block 1 (x-direction):     T = m₁a     (1)

     block 2 (y-direction):     m₂g - T = m₂a.    (2)

Solution. We are interested in T and must eliminate a from (1) and (2). Multiplying both sides of (1) by m₂ and multiplying both sides of (2) by m₁ gives

                     m₂T = m₁m₂a    (3)
and
                     m₁m₂g - m₁T = m₁m₂a.    (4)

Subtracting (4) from (3) gives

                     m₂ T - (m₁ m₂g - m₁T) = 0    (5)
whence
                     m₁T + m₂ T = m₁ m₂g    (6)
whence
                     T = [m₁ m₂ /( m₁+ m₂)] g .    (7)

Substituting the given mass values gives for the tension T in the string and the magnitudes of the forces exerted by the string on the two blocks:

                 T = T₁ = T₂ = [0.6x0.4/(0.6+0.4)] x 9.8 = 0.24 x 9.8 = 2.35 N .    (8)

If one has already found the magnitude of the acceleration, 3.92 m/s², it is very easy to get the tension by substituting into equation (1). Thus,

                 T = m₁a = 0.6 x 3.92 = 2.35 N.     (9)

Think About It.

1. The final expression (7) for the tension is dimensionally correct. The numerator of the fraction is a mass² and the denominator a mass. Thus, the ratio of the two is a mass. Multiplied by g, which has the units of acceleration, gives a force because mass times acceleration is a force. Thus, equation (7) is correct dimensionally.
2. Expression (7) is consistent with Answer (c) to Question 1 because it can be written

                T = m₁ /( m₁+ m₂) m₂g.    (10)

   Thus,    T < m₂g    since    m₁ /( m₁+ m₂) < 1.

3. When the mass m₂ goes to zero, one would expect the tension T to go to zero as well. Expression (7) is consistent with this.