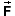 1,
1, 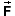 2, ... acting on a particle is equal to
the product of the particle's mass m and the particle's
acceleration
2, ... acting on a particle is equal to
the product of the particle's mass m and the particle's
acceleration 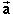 ,
,
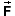 1 +
1 +
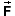 1 + ... = m
1 + ... = m 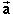 .
.
The sum of all forces1,
2, ... acting on a particle is equal to the product of the particle's mass m and the particle's acceleration
,
1 +
1 + ... = m
.
Comment 1. If the forces on the left-hand side of this equation are all real forces, then this equation is true only in an inertial frame, any inertial frame. In this Lesson, we will use the Laboratory Frame throughout which the applet takes to be an inertial frame. Real forces are forces resulting from the interaction between two objects.
Comment 2. "Particle" means a "point particle" of negligible extension. This law also applies to an extended object if the object is rigid and not rotating. Then all parts of the object have the same acceleration, and Equation (1) is true with this acceleration. It does not matter where the forces are acting on the object.
Comment 3. The sum of all forces acting on a particle or extended object is referred to as the net force or the total force acting on the particle or object. The net force is the vector sum of the individual forces.