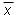In practice, one will have available only a finite set of measurement values from which to estimate the mean 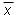and the standard deviation s of the entire distribution of infinitely many measurement values of x. (The "standard" symbol for the SD is the Greek letter s, read: "sigma".)

The sample mean m of n measurement values x_i where the subscript i runs from 1 to n is the arithmetic mean

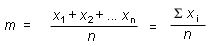
(1)

The S is the Greek captial letter sigma, and it means "the sum of all".

The sample mean m is the best estimate of the mean 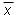available from the given finite sample.

The best estimate s for the standard deviation s, based on the sample from which m is calculated, is given by the following expression.

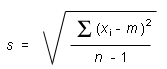
(2)

Expression (2) can be transformed into the following computationally more efficient expression:

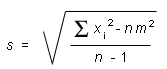
(3)

Comment. Expressions (2) and (3) for s contain n - 1 in the denominator. You may have expected to see n here. However, n - 1 is better because Expressions (2) and (3) use the sample mean m rather than the true mean 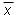. The deviations of the individual measurement values x_i from the sample mean are smaller on the average than the deviations from the true mean. One can prove that the smaller denominator n - 1 corrects for this exactly.

Page 9 will present an example calculation of s.