The SD is a measure of how far the individual data points (measurement values) scatter around the mean of the distribution. The greater the SD, the more spread-out the data are. This is reflected in the general definition of the SD:

Comments.

1. The symbolic expression on the right assumes that we are talking about the standard deviation of a quantity x.
2. The mean of a quantity is indicated by a bar over the quantity. So, the mean of the quantity x is indicated by .
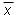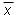3. In this definition, the mean and the mean of the squared deviations from the mean 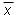are means over the distribution of infinitely many measurement values of the quantity x. These "true means" are not known if one has a finite set of, say, five measurement values, a so-called sample of the distribution. From such a sample one can only calculate sample means. (See Page 8.) The definition of the SD above is important theoretically, but cannot be used in practice.
4. The SD is also known as rms-deviation. "rms" stands for "root-mean-square". You will be able to understand this name when you look at the expression above.
5. The reason the deviations are squared in this definition is that the mean of the deviations themselves, not squared, would be zero because the deviations from the mean, on average, are equally much positive as negative. The final square root "corrects" for squaring the deviations. Also, with the square root in place, the units of the SD are the same as the units of the quantity that is being measured.

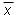Okay, now that the SD has been defined, how does one actually calculate it, or, more exactly, get a best estimate for it, given a sample of measurement values? Please go on to Pages 8 to 11 to find out. It will also be explained how to get a best estimate for the mean of the distribution and the standard deviation of the mean.