Meas. #	Value (m)
1	1.18
2	1.16
3	1.18
4	1.19
5	1.21
	m = 1.184 m   s = 0.018 m

1. We have calculated the sample standard deviation s in order to get a measure of the uncertainty of the individual measurement values. If you round the value of 0.018 m to 0.02 m, you get a result that can easily be obtained by "eye-balling" the five measurement values in the table above. Thus, what we have done may seem like cracking a walnut with a sledge hammer. And you would be right in feeling this way. If only a few data points are given, there is little to be gained by working out the SD. A quick estimate will usually be a good enough value of the uncertainty. However, if a much larger number of measurement values is available, the SD will give a better measure of the uncertainty. The purpose of the calculation done here was mainly to illustrate the procedure.

   Whether, in a case like this, you obtain an uncertainty of 0.02 m by "eye-balling" or an uncertainty of 0.018 m by calculating the standard deviation, in both cases the uncertainty would be denoted DL, if the quantity to be measured is denoted by the symbol L. Thus, you need to make it clear in the context what DL denotes, i.e., how DL was determined. Compare the section "Notation" on Page 1 of this session.

2. An uncertainty of 0.02 m for the individual measurement values with a sample mean of 1.18 m amounts to a relative uncertainty of about 2%. A 2%-uncertainty means that the measurement values are reasonably precise, but not very precise. There are measurements that are much more precise than that. E.g., physicists think that they have measured the mass of the electron to eight significant digits.
3. Insofar as the measurement values are reasonably precise, they are also reasonably accurate. However, accuracy requires more than a small scatter of individual measurement values. It also requires that the mean is close to the true value.

   Suppose the tape measure that was used to measure the lengths in the tabulation above had the first 10 cm missing, without this being noticed. This would make all measured values and their mean 10 cm too large. This kind of an error is called a systematic error. If a sizeable systematic error is present, the measurements would be correspondingly inaccurate even though fairly precise.

4. The sample mean m is the best estimate of the true value, if no systematic errors are present. If a systematic error is present, m may be substantially off the true value and it may be possible to get a better estimate of the true value by trying to correct for the systematic error if one has some information about it.
5. Suppose you take another set of five measurements of the length and yet another set, etc. Each time the sample mean will be a little bit different, but it will not scatter as widely as the individual measurement results. 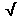If the individual measurement values are normally distributed, one can prove that the sample mean m too is normally distributed, with a standard deviation that is smaller than the SD of the individual measurement values by the factor of n.

   In the example above, the SD of the sample mean, s_mean, would be equal to s /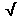n = 0.018 /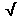5 = 0.008 m.

   s_mean = 0.008 m .

   If there is no systematic error present, the five measurement values thus provide the following final result for the length:

   1.184 m ± 0.008 m

   where the true mean 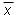has a roughly 68% chance of being in the indicated range.

   In quoting an uncertainty, make sure you indicate what the uncertainty means, whether it is the uncertainty in the individual measurement values or in the mean of these values. There is no generally accepted convention that dictates which uncertainty to use so that the reader of your publication needs to be informed.

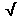6. The estimate s of the SD of the individual measurement values does not change with the sample size n, apart from the fluctuations to be expected with any change in the sample. However, the estimate s_mean = s /n of the SD of the sample mean decreases as the sample size n increases and would eventually approach zero as n approaches infinity.

   Can one make a measurement result arbitrarily accurate by going to larger and larger samples, at least in principle? Of course, there are practical limits to how often one can repeat a measurement.

   No, one cannot. E.g., one cannot go significantly farther in reducing the uncertainty than we have done here, simply by measuring more often. The final result quoted above already goes one decimal beyond the precision with which the individual measurement values are quoted. Going two decimals beyond this precision by increasing n would give a misleading impression of the accuracy of the result. The reason is that there is no assurance that there will not be a systematic error of the order of at least a few tenths of a centimeter inherent in the measuring procedure if the procedure can provide length values only to within 1 cm.