The following Activities are for the 'Charged Particle in Capacitor' applet. Make sure you know how the applet functions by consulting Help and ShowMe under Applet Help on the applet's Help menu.

ACTIVITY 1. The purpose of Activity 1 is to predict the kinetic energy of a charged particle upon impact of the particle on one of the plates of a parallel-plate capacitor after the particle has been released from rest at the other plate. Any forces other than the electric force are ignored.

RESET the applet. Display the Data box. Set the following parameters and the following initial conditions at t = 0 for the charged particle:

• electric field: E_y = -50 V/m;
• particle charge: q = 3 C;
• particle mass: m = 3.0 kg;
• drag the particle so that it touches the top plate;
• set the particle's velocity to 0.

With these settings, the direction of the electric field and of the electric force acting on the particle are downward. Display the force vector to verify this.

Make the following measurements with the applet:

(a) At t = 0, record

• the particle's y-coordinate (measured at the particle's center),
• the force acting on the particle.

(b) PLAY the motion until the particle hits the bottom plate. At this point, record the particle's

• y-coordinate (measured at the particle's center),
• kinetic energy KE,
• speed v.

Calculations

(a) The particle's y-coordinate when the particle is at the top plate depends on the size of your applet window. The taller the window, the more widely the plates are separated, and the larger the particle's y-coordinate at the top plate.

For the following sample calculations, let us assume y(0) = 185.0 m.

The force acting on a charged particle of charge q in an electric field is given by the expression

= q.(1)

For the values set above,

F_x = 0andF_y = 3×(-50) = -150 N.(2)

Compare Results (2) with the values given in the Data box. Note that the x-component of the force is zero, which means that the force is parallel to the y-axis. The minus sign in the value of F_y means the direction of the force is the same as that of the negative y-direction.

(b) When the particle is at the bottom plate, it is at y = 15.0 m. This is true independently of your window size.

Since the particle is moving parallel to the y-axis, the work W done on the particle in moving from the top to the bottom plate involves only the change Dy in the y-component of the particle's displacement. Thus, since the force is constant,

W = F_yDy = (-150)×(15.0 - 185.0) = 25,500 J.(3)

By the work-kinetic energy theorem, the particle's kinetic energy KE should change by W when the particle is moving from the top to the bottom plate. Therefore, since the particle's kinetic energy is zero at the top plate, at the bottom plate we have

KE_bottom = W = 25,500 J.(4)

Equating Value (4) to the expression for the kinetic energy, KE = (m/2)v², and solving for v, gives for the speed of the particle when the particle reaches the bottom plate:

v_bottom = 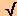(2KE/m) = 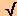(2×25,500/3) = 130.4 m/s.(5)

Repeat these calculations with the value of the displacement Dy that applies in your case, and compare the results with those given by the applet.

ACTIVITY 2. The purpose of this Activity is to perform similar observations and calculations as in Activity 1, but this time for a particle performing a kind of projectile motion, not a vertical drop.

Exercise 1. RESET the applet. Set E_y = -50 V/m, and keep the charge and mass at 3 C and 3.0 kg, respectively.

Display the Data and Energy boxes. Drag the particle to the bottom plate at x = 100 m, set the particle's speed to v = 200 m, and the velocity direction to q = 30^o relative to the positive x-axis. Display the velocity vector and the particle's path.

PLAY the motion. You should obtain a parabolic trajectory, first rising, then falling. REWIND the motion, and PLAY it again. Observe the kinetic energy column (leftmost column in the Energy box, entirely in red). Observe that while the particle is rising, the kinetic energy is decreasing, and that the opposite is true when the particle is falling. Is the kinetic energy zero when the particle is at the top of its path?

If the top of the kinetic energy column is beyond the top of the Energy box, rescale the height of the column by means of the Zoom slider inside the Energy box.

Exercise 2. Use the applet to determine the particle's kinetic energy approximately when the particle is at the top of its path. Do this by PLAYing the motion and stopping it as nearly as you can at the peak of the trajectory. STEPing the motion may help. Record the value of the kinetic energy from the Data box when the particle is near the peak.

Also determine the particle's y-coordinate at the peak using the value in the Data box.

Exercise 3. Calculate the kinetic energy at the bottom and at the peak.

Calculation of KE. At the bottom plate,

KE_bottom = (m/2)v² = (3/2)×200² = 60,000 J.(6)

The particle's x-component of velocity is constant because the x-component of the electric field and therefore the x-component of the force acting on the particle are zero. Thus, when the particle reaches the peak of its trajectory, its speed v_peak is not zero, but equal to the x-component of the particle's velocity. (The y-component of velocity is zero at the peak.) Thus, the particle's kinetic energy at the peak is equal to

KE_peak = (m/2)×v_x² = (m/2)×(v cos 30^o)²

= 3/2×(200×0.8660)² = 45,000 J.(7)

Exercise 4. Calculate the particle's elevation y_peak at the peak of the trajectory using the work-kinetic energy theorem.

Note on Work. The work W done on the particle by the electric force is given by Eq.(3) used earlier,

W = F_yDy (3)

Although Eq.(3) was obtained earlier for motions that are parallel to the y-axis and have no x-component, the equation also applies to general projectile motion in an electric field that is parallel to the y-axis. The reason is as follows. The general expression for W in two dimensions is

W = 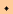D = F_xDx + F_yDy.(8)

In the present case of the capacitor, with the electric field parallel to the y-axis, the x-component of the electric force exerted on the particle is zero. Therefore, whether Dx is zero or not, the general expression (8) for the work done on the particle reduces to

W = F_yDy = qE_yDy.(9)

Eq.(9) is identical with Eq.(3). Therefore, Eq.(3) for W applies in all cases, no matter what motion the particle performs.

Using Eq.(1) to substitute for the electric force in Eq.(9) gives

W = F_yDy = qE_yDy(10)

Calculation of the particle's elevation at the peak. The calculation is based on the work-kinetic energy theorem. The work W done by the electric force on the particle involves the change in the particle's y-coordinate which in turn involves the particle's elevation at the peak. Thus, the work-kinetic energy theorem provides an equation for y_peak.

The work-kinetic energy theorem gives the equation

W = qE_y(y_bottom - y_peak) = KE_bottom - KE_peak.(11)

Substituting numbers gives

3×(-50)×(15 - y_peak) = 60,000 - 45,000(12)

y_peak = 15,000/150 + 15 = 115.0 m.(13)

Exercise 5. Repeat the preceding measurements and calculations for a different initial velocity.

Exercise 6. Repeat the preceding measurements and calculations for different values of the charge and mass of the particle and different values of the electric field.