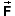1 acting on Particle 1 does work
W1 on Particle 1 and the kinetic energy of
Particle 1 changes by DKE1. Similarly for
Particles 2 to N.
The work-kinetic energy theorem for a system of particles
Let there be a system consisting of N particles, labeled 1
to N. Let us consider some time interval during
which the net force 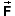1 acting on Particle 1 does work
W1 on Particle 1 and the kinetic energy of
Particle 1 changes by DKE1. Similarly for
Particles 2 to N.
The general work-kinetic energy theorem states that
W1 + W2 + ... +
WN = DKE1 + DKE2 + ... + DKEN.
(1)
Comment 1. In general, the work listed on the left-hand side of Eq.(1) contains work done both by internal and external forces. In the applet on Page 12, there are two internal forces, and the work done by these forces is not zero. There are no external forces. There are other systems in which there are only external forces and the work done by those is not zero. Finally, there are systems with both internal and external forces, and the work done by either kind of force on the system is unequal to zero.
Comment 2. Eq.(1) above for a system of particles is a straight-forward geneneralization of Eq.(1) on Page 1, which is the work-kinetic energy theorem for a single particle. Eq.(1) on this page is obtained from the work-kinetic energy theorem for a single particle simply by summing over all particles. For a proof of the work-kinetic energy theorem for a single particle see Energy/Work-Kin. En. Th'm/Explain It/Derivation.
The applet on Page 12
You can use the applet on Page 12 to investigate the work-kinetic energy theorem as it applies to a system consisting of two particles.
The system of two "particles" in the applet on Page 12 is a binary star system. Open "Activities Page 12" for suggestions on what to investigate with the applet.
Details on how to use the applet are available under Applet Help on the applet's Help menu.