Work-Kinetic Energy Theorem
Work-kinetic energy theorem for a single particle:
The net work W done on a particle during a given time
interval by the net force 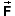 acting on the particle is equal to the change
in the particle's kinetic energy during that time interval.
In symbols,
acting on the particle is equal to the change
in the particle's kinetic energy during that time interval.
In symbols,
Wnet = DKE  (1)
(1)
where
KE = (m/2)v2  (2)
(2)
is the particle's kinetic energy, m the mass of the
particle and v the speed of the particle.
On Page 11, there is a statement of a generalized
work-kinetic energy theorem that applies to systems of more
than one particle. For a derivation of the work-kinetic
energy theorem, go to Energy/Work-Kin. En. Th'm/Explain
It/Derivation.
Contents of the 12-page session
Pages 1 to 10 will take you through several situations
involving one-particle systems. The applet on Page 12
simulates the motion of a two-particle system.
The first example, to be studied with the applet on Page 2,
involves a ball in vertical up-and-down motion without air
resistance, i.e., a ball in free fall. When you experiment
with the applet on Page 2, open the item "Activities Page 2"
under Related Items for suggestions on what to investigate
with the applet.
Details on how the applet on Page 2 functions are available
under Applet Help on the applet's Help menu.
Contents in detail
Page 1. Work-kinetic energy theorem for a single
particle. Table of Contents.
Page 2. Applet for investigating vertical free
fall.
Page 3. Application of work-kinetic energy theorem to
projectile motion.
Page 4. Applet for investigating projectile
motion.
Page 5. Application of work-kinetic energy theorem to
motion of a charged particle in a uniform electric field.
Page 6. Applet for investigating motion of a charged
particle in the uniform electric field of a parallel-plate
capacitor.
Page 7. Application of work-kinetic energy theorem to
a situation with non-constant force (circular motion with
constant or changing speed).
Page 8. Applet for investigating circular motion with
constant or changing speed.
Page 9. Application of work-kinetic energy theorem to
a particle moving subject to an arbitrary and variable force
that can be controlled by the user.
Page 10. Applet for investingating the motion of a
particle that is subject to a variable force.
Page 11. Work-kinetic energy theorem for a system of
several particles and application to a two-body system.
Page 12. Applet for investigating the motion of a
binary star system. (Qualitative investigation).
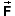 acting on the particle is equal to the change
in the particle's kinetic energy during that time interval.
In symbols,
acting on the particle is equal to the change
in the particle's kinetic energy during that time interval.
In symbols,
![]() (1)
(1)
![]() (2)
(2)