Contents
![]() Work-kinetic energy theorem for a single
particle
Work-kinetic energy theorem for a single
particle
![]() Derivation of the work-kinetic
energy theorem for a single particle
Derivation of the work-kinetic
energy theorem for a single particle
![]() Work-kinetic energy theorem for a system
of particles
Work-kinetic energy theorem for a system
of particles
The work-kinetic energy theorem for a single particle
The net work W done on a particle during a given time interval by the net forceacting on the particle is equal to the change in the particle's kinetic energy during that time interval. In symbols,
W = DKE = D[(m/2)v2]
(1)
where m is the mass of the particle and v the speed of the particle.
may vary during the given time interval.
Derivation of the work-kinetic energy theorem for a single particle
1. Constant net force
If the net force 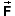 acting on a particle is constant, the particle's
acceleration
acting on a particle is constant, the particle's
acceleration 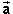 is constant as well, according to Newton's second law.
is constant as well, according to Newton's second law.
There is a standard equation in the kinematics of motion with constant acceleration,
2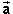
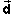 = Dv2,
= Dv2,![]() (2)
(2)
which relates the particle's displacement 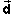 to the change in the square of
the particle's speed v during a given time interval. For
more details, see Page 2 of "Acceleration" under Related Items.
to the change in the square of
the particle's speed v during a given time interval. For
more details, see Page 2 of "Acceleration" under Related Items.
The dot between 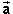 and
and 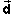 in Eq.(2) indicates the scalar product (dot product) between
the two vectors. You can look up "Scalar Product" under
Related Items.
in Eq.(2) indicates the scalar product (dot product) between
the two vectors. You can look up "Scalar Product" under
Related Items.
Multiplying both sides of Eq.(2) by m/2, where m is the mass of the particle, gives
(m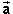 )
)
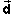 = D[(m/2)v2].
= D[(m/2)v2].![]() (3)
(3)
The factor m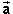 on the left-hand side is equal to the net force
on the left-hand side is equal to the net force
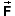 , and the
right-hand side is equal to the change in the kinetic energy
KE (KE = (m/2)v2).
Thus,
, and the
right-hand side is equal to the change in the kinetic energy
KE (KE = (m/2)v2).
Thus,
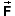
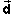 = DKE.
= DKE.![]() (4)
(4)
The left-hand side of Eq.(4) is called the net work done
on the particle. Thus, using the symbol W to denote net
work, the net work done by a constant net force 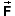 is given by
is given by
W = 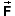
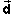 .
.![]() (5)
(5)
With this notation, the work-kinetic energy theorem can be written
W = DKE.![]() (6)
(6)
Eq.(6) with Eq.(5) for W is the work-kinetic energy
theorem for a single particle when acted upon by a constant
net force. The theorem says that the work done by the net force in some
time interval during which the particle undergoes the
displacement 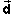 is
equal to the change in the particle's kinetic energy during that
time interval.
is
equal to the change in the particle's kinetic energy during that
time interval.
2. Variable net force
If the net force 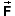 acting on a particle varies, either in direction or
magnitude, Eq.(4) and Expression (5) for the net work W
do not apply. The reason is that Eq.(4) is based on Eq.(2) which
assumes a constant acceleration during a finite time
interval. The acceleration is not constant if the net force is
not constant.
acting on a particle varies, either in direction or
magnitude, Eq.(4) and Expression (5) for the net work W
do not apply. The reason is that Eq.(4) is based on Eq.(2) which
assumes a constant acceleration during a finite time
interval. The acceleration is not constant if the net force is
not constant.
However, the net force and the acceleration are constant during
any infinitesimal time interval. Therefore, Eq.(4) does
apply to such an interval if one replaces the finite
displacement 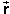 , and
the finite change DKE in
kinetic energy by an infinitesimal change
dKE. Thus,
, and
the finite change DKE in
kinetic energy by an infinitesimal change
dKE. Thus,
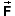
 d
d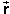 = dKE.
= dKE. ![]() (7)
(7)
On the left-hand side of Eq.(7) is the infinitesimal net work
dW done on the particle while the particle undergoes the
infinitesimal displacement d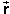 ,
,
dW = 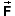
 d
d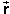 .
. ![]() (8)
(8)
With this notation, Eq.(7) can be written
dW = dKE .![]() (9)
(9)
Eq.(9) combined with Expression (8) for dW is the work-kinetic energy theorem for an infinitesimal time interval. The theorem applies to situations with arbitrarily varying forces.
What about finite time intervals when the force is varying?
The net work W done on the particle during a finite time interval is the sum of all the infinitesimal amounts of work dW done during the infinitesimal intervals that make up the finite interval. Similarly, the overall change DKE in kinetic energy during the finite time interval is the sum of the infinitesimal changes dKE during the infinitesimal intervals. Since Eq.(9) holds for each infinitesimal time interval, summing the infinitesimal changes dW and dKE that occur during the finite time interval again gives us Eq.(6),
W = DKE.![]() (6)
(6)
Thus, Eq.(6) expresses the work-kinetic energy theorem in general, for either a variable or a constant net force. The only difference between the two cases lies in how the net work W is calculated. In general, one has to calculate W by summing the infinitesimal amounts of work dW given by Eq.(8). In the case of a constant net force, this sum results in Expression (5) so that one can simply use this final expression for W.
Technically, the sum W of infinitely many infinitesimal amounts dW on the left-hand side of Eq.(6) is what is called an "integral". Calculus provides rules for working out such integrals.
The work-kinetic energy theorem for a system of particles
Eq.(6) above also expresses the work-kinetic energy for a system of particles, except that W now is the total work done on all particles of the system and KE is the total kinetic energy of all particles of the system.
In more detail, the work total W done on a system of
particles and the total kinetic energy KE of a system
are defined as follows. Let the system consist of N
particles, labeled 1 to N. Let us consider some time
interval during which the net force 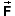 1 acting on Particle 1 does work
W1 on Particle 1 and the kinetic energy of
Particle 1 changes by DKE1. Similarly for
Particles 2 to N. Then
1 acting on Particle 1 does work
W1 on Particle 1 and the kinetic energy of
Particle 1 changes by DKE1. Similarly for
Particles 2 to N. Then
W = W1 + W2 + ... +
WN ![]() (10)
(10)
KE = KE1 + KE2 + ... +
KEN. ![]() (11)
(11)
To derive the work-kinetic energy theorem for a system of particles, all one has to do is write down Eq.(6) separately for each particle and sum the resulting N equations.
Comment. When dealing with a system of particles, one distinguishes between internal and external forces acting on the particles of the system. Internal forces are forces exerted on a particle by other particles of the system, and external forces are forces exerted on a particle by objects that are not part of the system.
One can write the total work done on the system as the sum of the total work done on all particles by the internal forces, Wint, and the total work done on all particles by the external forces, Wext,
W = Wint + Wext. ![]() (12)
(12)