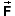
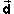 = Fd cos θ
= Fx dx +
Fy dy
= Fd cos θ
= Fx dx +
Fy dyWork done by a variable force: general definition
The work W done by a constant force on a system is defined by
W = 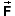
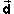 = Fd cos θ
= Fx dx +
Fy dy
= Fd cos θ
= Fx dx +
Fy dy![]() (1)
(1)
The vector 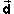 is
the displacement of the point at which the force is
acting. For details, please see Page 2.
is
the displacement of the point at which the force is
acting. For details, please see Page 2.
If the force 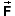 varies while the displacement
varies while the displacement 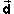 occurs, either in magnitude or direction, Eq.(1)
does not apply. Eq.(1) requires a definite force vector, but
there is no one force vector that one could use during the
entire time interval while the displacement
occurs, either in magnitude or direction, Eq.(1)
does not apply. Eq.(1) requires a definite force vector, but
there is no one force vector that one could use during the
entire time interval while the displacement 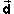 is occurring if the force is
varying.
is occurring if the force is
varying.
However, although a force may be varying during a finite
time interval, during an infinitesimal time interval it
cannot be anything but constant. There is not enough time for
the force to change during such an interval. Therefore, Eq.(1)
does apply to an infinitesimal time interval during which the
point at which the force is acting undergoes an infinitesimal
displacement d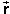 . The corresponding infinitesimal work dW
done by the force on the system is defined by
. The corresponding infinitesimal work dW
done by the force on the system is defined by
dW = 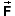
 d
d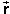 = F|d
= F|d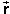 | cos θ
= Fxdx +
Fydy.
| cos θ
= Fxdx +
Fydy.![]() (2)
(2)
In three dimensions, a third term Fzdz needs to be added on the right-hand side of Eq.(2). In one dimension, if the motion is along an x-axis, the term Fxdx is sufficient.
The net work W done on the system during a finite time interval is the sum of all the infinitesimal amounts of work dW done during the infinitesimal intervals that make up the finite interval. The path taken by the point at which the force is acting will in general be curved. The infinitesimal amounts of work dW need to be calculated for the infinitesimal displacements that make up this curved path.
Technically, the sum W of infinitely many infinitesimal amounts dW is what is called an "integral". Calculus provides rules for working out such integrals.