The CM-work theorem for a system, or for an object that may be deformable, is analogous to the work-kinetic energy theorem for a single particle. The differences are that the net work must be replaced by net CM-work and that the kinetic energy of the particle must be replaced by translational kinetic energy of the system or object. (CM stands for center of mass.)

CM-Work Theorem For A System

The theorem says that the CM-work W_CM,net done by the net external force acting on a system or object is equal to the change in the translational kinetic energy of the system or object. In symbols,

W_CM,net = Δ[M/2 V²](1)

where M is the mass of the system or object and V the speed of the CM of the system. For a definition of CM-Work, go to CM-Work under Related Items.

Comments

1. Only the CM-work done by the external forces is needed in Equ.(1). The total CM-work done by all internal forces is zero because in calculating the CM-work all forces get multiplied by the same displacement, that of the CM, and because the sum of all internal forces is zero by Newton's third law. In contrast, the work done on a system by all internal forces is not zero in general because the points at which the forces are acting undergo different displacements so that a common displacement cannot be factored out.
2. The quantity (M/2)V² is called translational kinetic energy of the system or object. It is sometimes also called kinetic energy of the CM, for obvious reasons. However, in using the latter name one must realize that it has no literal meaning because the CM of a system of particles or of an arbitrarily shaped object is a fictitious point at which no mass may reside at all and that therefore cannot have true kinetic energy either.
3. A system of particles or an extended body can have other kinetic energies besides the translational kinetic energy (M/2)V² if the particles comprising the system or body perform motions relative to the CM, in addition to the motion that they share with the CM.
4. The work-kinetic energy theorem for a single particle is a special case of the CM-work theorem. For the case of a single particle, the position of the CM is identical with the position of the particle, the forces acting on the particle are necessarily external forces, and the net CM-work done is identical with the net work done.

Example

Suppose a skater is pushing off a wall, as in the illustration below, and that the wall exerts a constant force 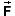on the skater where the wall is in contact with the skater's hand.

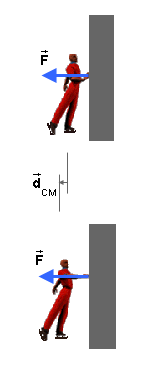
The illustration shows the skater initially when the skater is at rest and at a later instant when the skater's CM has undergone the disp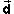lacement _CM. The skater is in contact with the wall throughout this displacement.

The CM-work done by the wall on the skater is equal to Fd_CM. By the CM-work theorem, assuming the skater glides with negligible friction so that there is no CM-work done on the skater by friction, Fd_CM is equal to the change in the skater's translational kinetic energy or, since the skater started from rest, equal to the skater's translational kinetic energy (M/2)V² at the end of the displacement,

Fd_CM = (M/2)V² . (2)

If one knows the magnitude d_CM of the displacement of the skater's CM and knows the skater's speed V at the end of the displacement, one can use this equation to calculate the magnitude of the force exerted by the wall on the skater.

Comment. In contrast to the CM-work theorem, the work-kinetic energy theorem for systems or extended objects provides no useful information when applied to the skater. The reason is that it involves the work done by all forces, external and internal, and includes all forms of kinetic energy, not only the translational kinetic energy of the system. We have no information about either the work done by the internal forces nor the kinetic energies of the parts of the system or object relative to the CM.