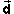On Page 4 we have calculated the magnitude of the overall displacement vector 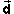= (-35, 20) m to be equal to d = 43.0 m. Now let us calculate the direction angle q of this vector, measured in the positive (counter-clockwise) sense relative to the positive x-axis.

It is very useful to make a drawing when working with angles.

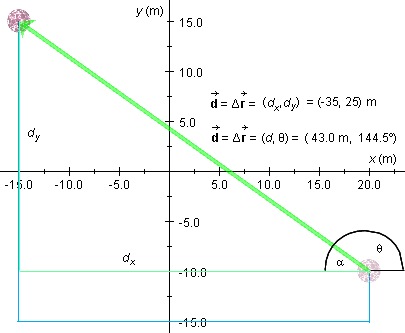
The diagram shows the displacemen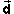t and its scalar components d_x and d_y in green and the path traveled in blue. The angle q is shown, as well as the supplementary angle a. We will calculate a first.

The two scalar components d_x and d_y form the two sides in a right-angle triangle opposite to the hypotenuse. Angle a is opposite to d_y. Therefore, by the definition of the tangent,

tan a = |d_y / d_x| = |25/-35| = 0.7143 .

This implies

a = tan^-1 0.7143 = 35.5^o.

The supplementary angle q is equal to

q = 180^o - a = 180^o - 35.5^o = 144.5^o.