Answers to the May 30, 1997 Question

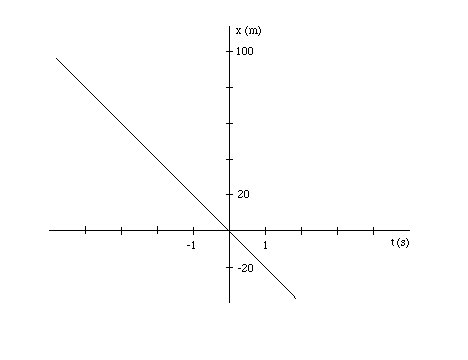
Question

Physics 211 - (This is a challenge question. It contains concepts that you are not expected to have studied before beginning the course.) Let us consider once more the car from the May 16 question. The position x of the car as a function of the time t could be described by the equation x = -20t + 20. (Analytical Geometry. Graphs.)

Suppose you have a reference frame, called the car's frame, in which this car is at rest, i.e., a reference frame that is moving at the car's velocity relative to the road. The frame in which the road is at rest is called the road's frame. In the car's frame, the car's position is constant. Let x' denote the position coordinate in the car's frame. (x is the position coordinate in the road's frame.) Let us choose the origin of the car's frame, x' = 0, so that the constant position of the car in this frame is equal to x' = 20 m, at all times.

Hint: You can think of the car's frame as an (infinitely) long ruler rigidly attached to the car, aligned with the direction in which the car is moving, and moving with the car. The ruler is used for measuring the positions of objects. Thus, to determine the value of the position of an object in the car's frame at a given time, i.e., the object's x'-value at that time, one simply records where on the ruler the object is at that time. The car itself is at x' = 20 m on this ruler. The origin of the ruler is outside of the car.

Part (a).Using the same set of x,t axes as for the x vs. t graph of the motion of the car in the May 16 question, show the x vs. t graph of a second car that is at rest at the origin of the car's frame, i.e., for which x' = 0 at all times.

Answer to Part (a)

The equation x = -20t + 20 implies that in the road's frame the car is at x = 20 m at time t = 0. Since in its own frame the car is at x' = 20 m at all times, including at t = 0, the primed and unprimed position coordinates of the car are equal at t = 0. This implies that x' = x for all points at t = 0, not only for the point where the car happens to be, because the distances between any two points at a given instant are the same in both frames.

The x'-axis is moving relative to the x-axis with a velocity equal to -20 m/s. This means that the origin of the x'-axis is at x = -20t at time t. Therefore a point with x-coordinate x will have an x'-coordinate x' = x + 20t at time t. (Note that it is +20t, not -20t, in this equation. The reason for this will become clear if you draw a picture of the two axes side-by-side at some time t > 0 that shows the two origins x = 0 and x' = 0 and shows a given point with x-coordinate x. Remember that this is a challenge question. So there are a few things left for you to figure out on your own.)

The equation

lets you calculate the x'-coordinate of a point at time t whose x-coordinate at time t is known, and vice versa.

We are given that the second car has x' = 0 at all times. Substituting this value into equation (1) gives us the equation

for the second car. This is a straight line through the origin of an x,t coordinate system. This line is parallel to that for the first car because both cars have the same velocity, namely, -20 m/s. (The velocity is equal to the slope of an x vs. t graph.) See the following diagram.

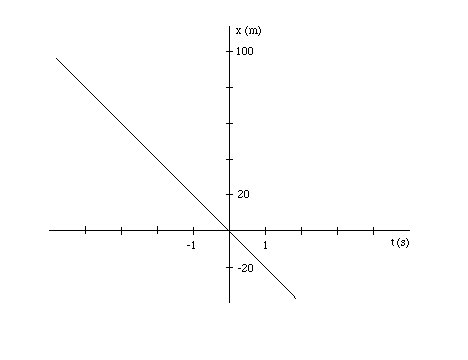
Part (b).Do the same as in part (a), but for a car that is at rest at x' = 40 m.

Answer to Part (b)

Substituting x' = 40 m into equation (1) and solving for x gives

The graph of this equation is a straight line parallel to the straight line in the preceding two graphs, but intersecting the x-axis at x = 40 m. See the following diagram.

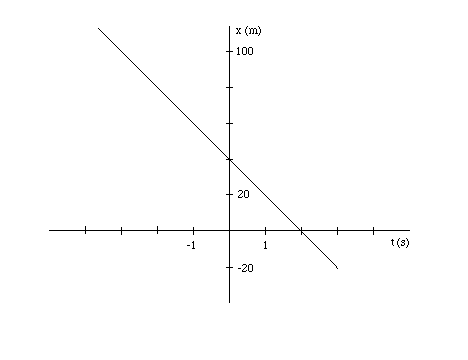
Part (c).What are the distances between the three cars (i) in the frame in which the road is at rest and (ii) in the car's frame?

Answer to Part (c)

The three cars are spaced at distances of 20 m. These spacings are the same in both frames, because distances between points are the same in the two frames, and the distances stay the same in time because all three cars are moving with the same velocity.