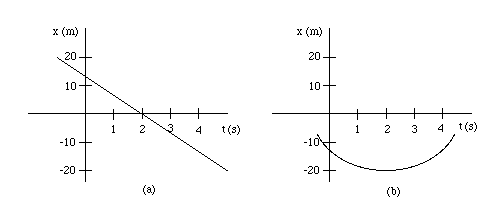
Question
Physics 211 - For the following two graphs of position x vs. time t, determine the values of the velocity at t = 2 s and t = 4 s. (Graphs.)
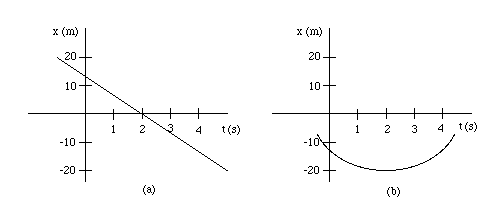
For graph (a), it should be possible to come up with a fairly accurate value of the velocity v. However, for graph (b), one can determine only a pretty rough value. In case (b), it may help if you hold a ruler against the screen.
Hint: Remember that the velocity at a time t is equal to the slope of the position vs. time graph at that time t. The slope of a graph at a given point is equal to the slope of the tangent to the graph at that point. In the case of a straight-line graph, the tangent is identical with the straight line. In the case of a curved graph, the tangent at a point is the straight line that touches the graph at that point, but does not intersect it.
Answer
Graph (a). For a straight line graph, the slope has the same value everywhere, equal to the ratio rise/run of the straight line. The velocity values at t = 2 s and t = 4 s are both equal to this slope.
The following diagram shows graph (a) with a rise-run triangle (dashed) to calculate the slope.
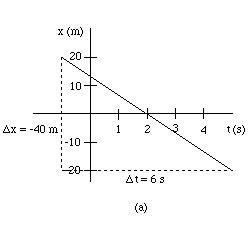
We make the rise-run triangle as large as possible to get as accurate a value for the slope as possible. The "rise" Dx is equal to -40 m because x changes from 20 m to -20 m as we go from left to right along the graph. The corresponding run is Dt = 6 s because t changes from -1 s to 5 s as we go from left to right along the graph.
Thus, the slope of the straight line, and therefore the velocity v at both t = 2 s and t = 4 s, is equal to
Graph (b). For a curved graph, the slope has different values at different points of the graph.
At t = 2 s, the x vs. t graph is horizontal. Thus, the slope and therefore the velocity is 0 at t = 2 s.
The diagram below shows graph (b) with a tangent drawn at the point t = 4 s. The tangent is shown as a solid line. A rise-run triangle to determine the slope of this tangent is shown with dashed lines.
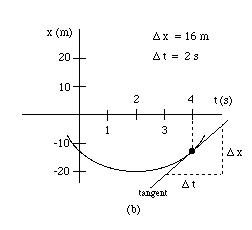
As you can see, for a run Dt of 2 s, as t changes from 3 s to 5 s, the rise Dx is approximately 16 m, as x changes from -20 m to - 4 m.
Thus, the slope of the graph at t = 4 s, and therefore the velocity at this instant, is equal to