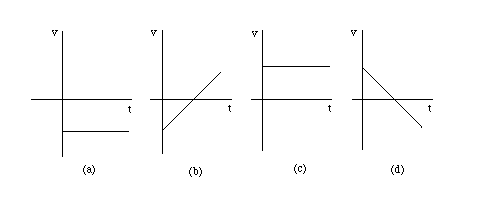
Past questions issued on August 1, 1997, August 8, 1997, and August 15, 1997 are listed below.
Physics 211 - In the July 18 and 25, 1997 questions you were asked to start from a displacement vs. time graph and find the corresponding velocity vs. time graph. Today you will be asked to do the opposite. (Graphs.)
Consider once more the four velocity vs. time graphs shown below.
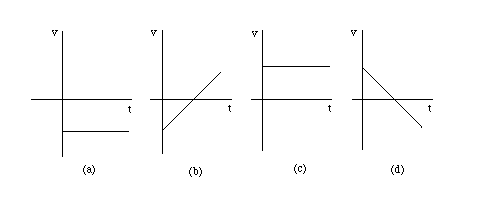
For each of the four cases (a) to (d), draw (i) the corresponding displacement vs. time graph that has Dx = 0 at t = 0, (i) a position vs. time graph that has x = 10 m at t = 0, and (iii) a position vs. time graph that has x = -10 m at t = 0.
Hint: Review the answer to the July 25, 1997 question.
Answer.
Physics 211 - For the following two graphs of position x vs. time
t, determine the values of the velocity at t = 2 s and t = 4
s. (Graphs.) For graph (a), it should be possible to come up with a fairly
accurate value of the velocity v. However, for graph (b), one can
determine only a pretty rough value. In case (b), it may help if you
hold a ruler against the screen. Hint: Remember that the velocity at a time t is equal to the slope
of the position vs. time graph at that time t. The slope of a graph
at a given point is equal to the slope of the tangent to the graph at
that point. In the case of a straight-line graph, the tangent is
identical with the straight line. In the case of a curved graph, the
tangent at a point is the straight line that touches the graph at that
point, but does not intersect it.
Physics 211 - Suppose that a particle moves with constant velocity
v = -15 m/s along an x-axis and that it passes the point x = 20 m at t
= - 1 s. Where will the particle be at t = 3 s? Solve this problem
both analytically, i.e., by calculation, and graphically. Also derive an expression for the general position x of the
particle at the general time t. In addition, make a diagram that
shows the x-axis and the particle's positions on the x-axis at t = -1
s and t = 3 s. (Definition of velocity. Analytical geometry.
Graphs.)
August 8, 1997
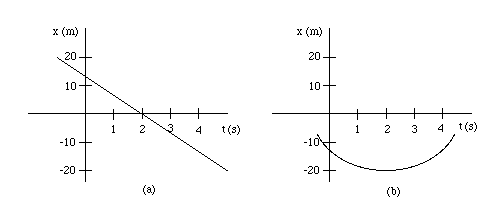
August 15, 1997
Return to
Top of
page.