Past questions issued on July 5, 1996, July 12, 1996, July 19, 1996, July 26, 1996, and August 2, 1996 are listed below.
For this week's question, you need to have a bit of background on vectors. You may not have studied vectors before. In that case, look up vectors for a brief introductory lesson that will provide the necessary background including an explanation of the notation used here. You should also review the July 19 question.
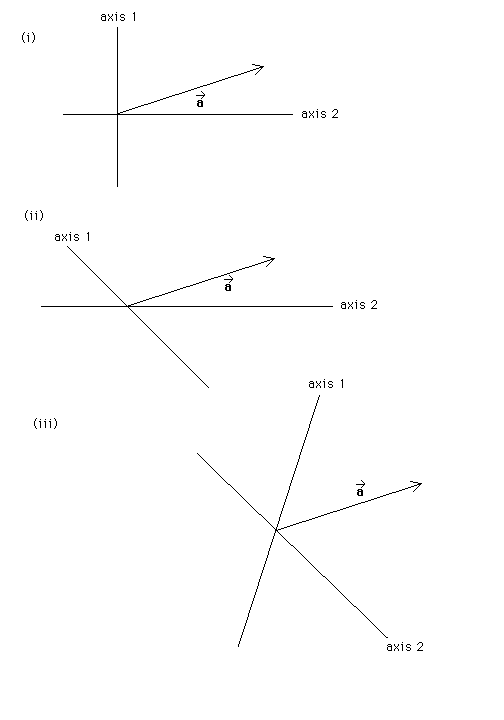
Parts (i), (ii), and (iii) of the following diagram each show the same vector a* and two axes, labelled 1 and 2. The two axes are different in each case. In each case, construct two vectors, a1* and a2*, such that a1* is oriented along axis 1 and a2* along axis 2 and such that a1* + a2* = a*. (Vectors).

For this week's questions, you need to have a bit of background on vectors. You may not have studied vectors before. In that case, look up vectors for a brief introductory lesson that will provide the necessary background including an explanation of the notation used here. You should also review the July 19 question.
(a) The difference between two vectors a* and b* is defined as a* - b* = a* + (-b*). For each of the three pairs of vectors shown in diagram (e) of the July 19 question, parts (i) to (iii), determine the difference a* - b*. The diagram is reproduced below.
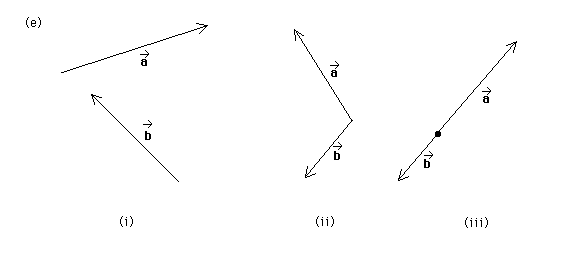
(b) In the answer to part (b) of the July 19 question, it was pointed out that one can add two vectors by joining them tail to tail, constructing a parallelogram with the two vectors as sides, and then drawing one of the two diagonals in the parallelogram. Show that the difference a* - b* is represented by the other diagonal and determine the direction one should assign to this diagonal.
Answer.The following questions are related to the addition of vectors. You may not have studied vectors before. In that case, look up vectors for a brief introductory lesson that will provide the necessary background.
Question (a). Diagram (e) below shows three pairs of vectors a* and b*. For each case, find the sum of these two vectors. In the case of pair (iii), both vectors have their tail ends at the dot.

The following questions involve small proofs. All proofs should be based on the graphical construction of a vector sum explained above.
Question (b). Show that vector addition is commutative, i.e., that a* + b* = b* + a*, for any two vectors a* and b*.
Answer.Question (c). Show that vector addition obeys the associative law, i.e., that (a* + b*) + c* = a* + (b* + c*).
Answer.Question (d). There exists a vector called the 'null vector' and denoted 0 (without an arrow above the symbol 0; this null vector is not, however, the same as the number 0; this notation is, therefore, not ideal). When the null vector is added to any given vector a* the result is again that vector, i.e., a* + 0 = a*. Find the arrow that would represent the null vector.
Answer.Question (e). For any given vector a*, there exists another vector denoted -a* such that a + (-a*) = 0. (Here, 0 denotes the null vector because the sum of two vectors is again a vector.) Draw a vector a* and find the corresponding vector -a*.
Answer.When learning a new subject, it is excellent practice to vary a question on the subject to which one already knows the answer.
Last week's question was a variation of the June 28 question that involved a change in the orientation of the parabolic mirror, but not an essential change in the physical situation. This week's question will be another variation of the June 28 question, but this time it will be a variation in the physical situation.
Physics 215 - Suppose the parabolic mirror is oriented as in the June 28 question as in the diagram below. This time, however, the rays are incident from the right. One such ray is shown. Now the mirror acts like a convex mirror (mirror bulging towards the incoming rays) while in the June 28 and July 5 questions it acted like a concave mirror (it looks like a 'cave' to the incoming rays.)
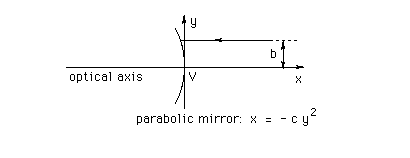
Prove that all rays incident on the mirror parallel to the optical axis are reflected so that they seem to be coming from one and the same point on the optical axis, which is again called the focal point. Find the distance between this focal point and the vertex of the mirror. (Geometry.)
Hint. It is not necessary to repeat the calculations that were done in the June 28 question. Given the result obtained in that case, one can obtain the answer to the present case by comparing the geometry of the present configuration to that of the June 28 case.
Answer.When learning a new subject, it is excellent practice to vary a question on the subject to which one already knows the answer.
Try this technique by varying the last question, the June 28 question. One variation is suggested below. In addition, try to make a variation of your own and then work out the answer.
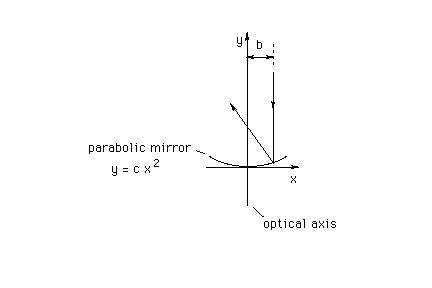
Question. Physics 215 - Suppose a parabolic mirror is oriented as in the diagram below, i.e., turned 90 degrees relative to the orientation of the mirror in the June 28 question. You might ask yourself what equation would now describe the shape of the mirror. The answer is given in the diagram. Given this mirror, prove again that all rays incident on the mirror parallel to the optical axis are reflected so that they go through one and the same point on the optical axis, the focal point, which is a distance 1/(4c) away from the vertex of the mirror. (Analytical Geometry. Algebra.)