Past questions issued on May 31, 1996, June 7, 1996, June 14, 1996, June 21, 1996, and June 28, 1996 are listed below.

Physics 215 - This is a difficult question. However, the individual steps that are required are of the same kind as in the preceding June 21 question.
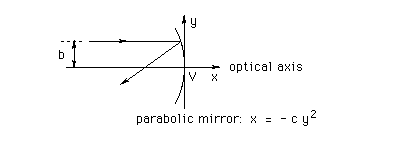
The diagram above shows a parabolic mirror and a ray incident on the mirror parallel to the optical axis. The optical axis is a line through the center (or vertex) V of the mirror such that the mirror is symmetrically positioned around this axis. The incident ray is a distance b away from the optical axis and is reflected by the mirror according to the law of reflection. (See the June 14 question.) (Analytical Geometry. Algebra.)
(a) Suppose the equation describing the shape of the mirror in terms of x and y coordinates is that given in the diagram above. Show that the point where the reflected ray intersects the optical axis is a distance f = 1/(4c) away from the vertex V of the mirror.
Hint. In order to deal with reflection by a curved mirror, you can pretend that the mirror acts like a plane mirror at the point of contact with the incident ray, where the slope of the plane mirror is equal to the slope of the curved mirror at this point. The slope of the parabolic mirror at a point whose y-coordinate is equal to b is equal to -1/(2cb). (This result can be derived easily if one knows some calculus. Here, you may just use it without deriving it.)
Hint. You also will need the slope of the normal to the mirror at the point where the incident ray hits the mirror. If this slope is denoted by n and if the slope of the mirror at the point where the normal is taken is denoted by m, then n is given by n = -1/m. To see how the slope n of the normal is related to the slope of the reflected ray, see the second solution to Part (b) of the June 21 question.
Answer.(b) The distance f at which the reflected ray intersects the x-axis does not depend on the distance b of the incident ray from the optical axis. What is the physical interpretation of this fact?
Answer.Physics 215 - The physical situation is the same as in Part (a) of the June 14 question. See the diagram below and the June 14 question. Again, a horizontal ray of light is reflected by a plane mirror. The incident ray is a distance b = 10.0 cm away from the horizontal x-axis. The mirror is inclined relative to the vertical y-axis by the angle alpha = 20.0 degrees. The origin of the x,y coordinate system is placed at the point where the mirror intersects the x-axis.
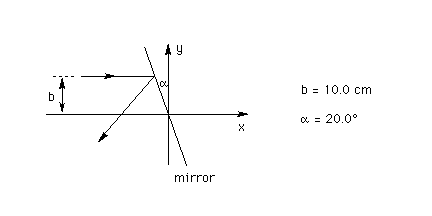
(a) What are the x and y coordinates of the point at which the incident ray hits the mirror? (Analytical geometry.)
Answer.(b) What is the slope of the reflected ray? (Analytical geometry.)
Answer.(c) At what distance from the origin of the x,y coordinate system does the reflected ray intersect the x-axis? (Analytical geometry.)
Answer.(a) Physics 215 - Diagram (a) below shows a plane mirror reflecting a ray of light. The diagram shows a horizontal reference axis (dashed horizontal line intersecting the mirror) and a vertical reference line (dashed). A horizontal ray of light is incident on the mirror and then reflected as shown in the diagram.
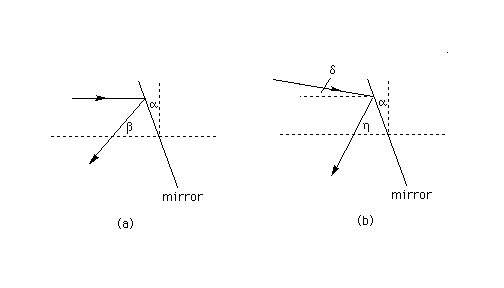
The mirror is inclined by an angle alpha relative to the vertical. Derive an expression for the angle beta between the reflected ray and the horizontal reference axis in terms of the angle alpha.
Hint: The law of reflection says that the angle of incidence is equal to the angle of reflection. These are the angles between the normal to the mirror and the incident and reflected rays, respectively. The normal to the mirror is the direction perpendicular to the mirror. (Geometry.)
Answer.(b) Physics 215 - Part (b) asks the same question as Part (a) except that now the incident ray forms an angle delta with the horizontal, as illustrated in Diagram (b) above. Find an expression for the angle eta between the reflected ray and the horizontal in terms of the angles alpha and delta. (Geometry).
Answer.Physics 205, Physics 215, Astronomy 211 - This question provides practice on the use of the trigonometric functions in right-angle triangles.
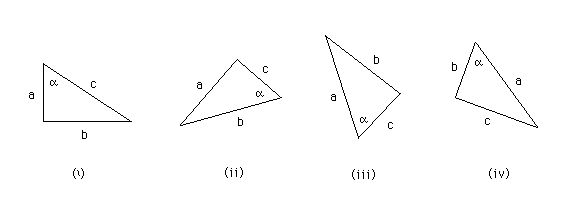
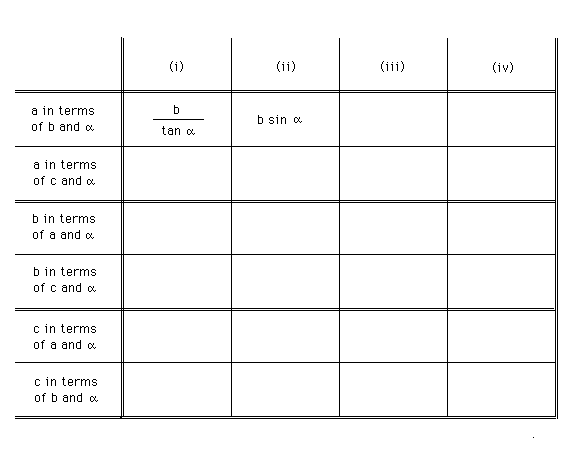
Each of the four triangles above contains a right angle. The three sides are labelled a, b, and c in no particular order. One of the two angles that is not a right angle is labeled by the Greek letter alpha.
The three most commonly used trigonometric functions are the sine, the cosine, and the tangent. These are the trig functions that you will find on all scientific pocket calculators.
For each of the four triangles (i) to (iv), express one of the three sides in terms of one of the other sides and an appropriate trig function evaluated for alpha. E.g., in the first row of the table below, you are asked to write down expressions for side a in terms of side b and angle alpha. The answers for triangles (i) and (ii) are shown in the table below. Fill in all other slots. (Trigonometry and algebra.)
(a) Physics 205, Physics 215, Astronomy 211 - A gardener lays out his garden on the north side of his house. The ridge of the house is oriented east-west and is 8.0 m above the level of the garden. The part of the garden closest to the house is 6.0 m away in the horizontal direction from the ridge of the house.
Will all of the garden be in the sun when the sun is in the south and 55 degrees above the horizon? (Trigonometry.)
Answer.(b) Physics 215, Astronomy 211 - How high in the sky, i.e., how many degrees above the horizon, will the sun be at noon on the longest day of the year, June 21st, in Calgary? (Geometry.)
Data: The latitude of Calgary is 51.0 degrees. The earth rotates once per day around an axis that is inclined by 23.5 degrees relative to the plane in which the earth orbits around the sun.
Answer.