For this week's questions, you need to have a bit of background on vectors. You may not have studied vectors before. In that case, look up vectors for a brief introductory lesson that will provide the necessary background including an explanation of the notation. You should also review the July 19 question.
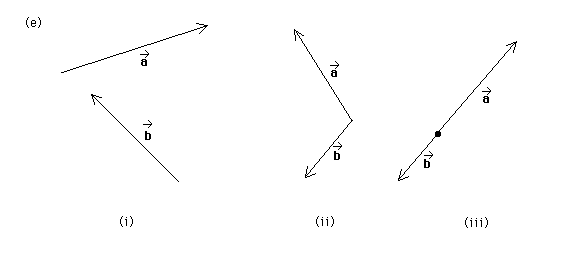
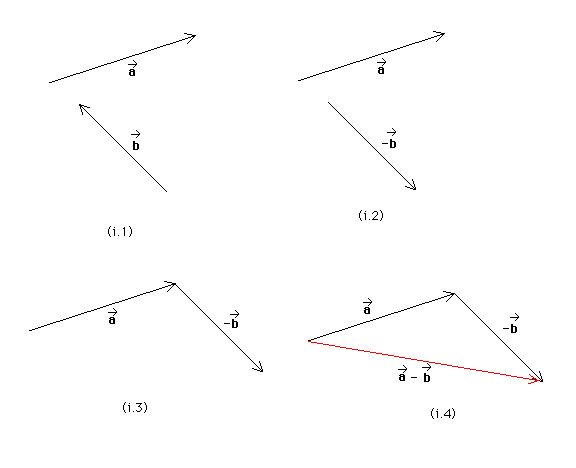
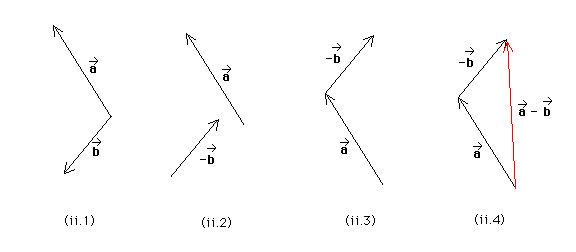
Question (a). The difference between two vectors a* and b* is defined as a* - b* = a* + (-b*). For each of the three pairs of vectors shown in diagram (e) of the July 19 question, parts (i) to (iii), determine the difference a* - b*. The diagram is reproduced below.

Answer. Each of the following three diagrams shows (1) the vectors a* and b*, (2) the vectors a* and -b*, (3) the vectors a* and -b* joined head-to-tail (head of a* joined to tail of -b*), and (4) the resultant a* - b* = a* + (-b*).
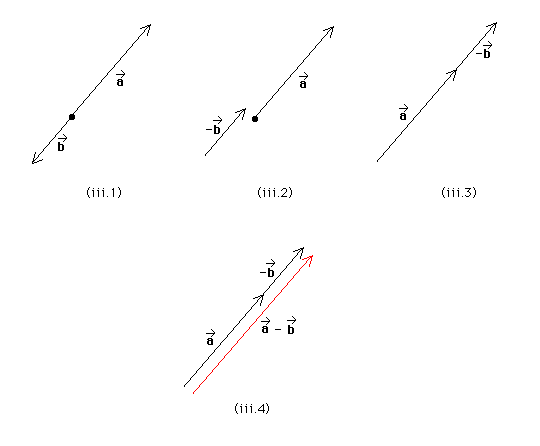
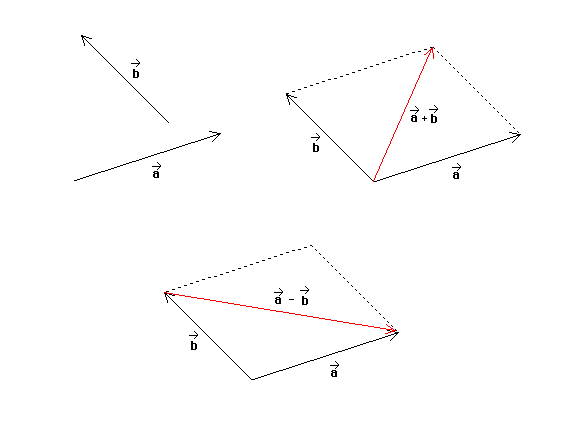
Question (b). In the answer to part (b) of the July 19 question, it was pointed out that one can add two vectors by joining them tail to tail, constructing a parallelogram with the two vectors as sides, and then drawing one of the two diagonals in the parallelogram. Show that the difference a* - b* is represented by the other diagonal and determine the direction one should assign to this diagonal.
Answer. The following figure shows the vectors a* and b* from diagram (e.i) of the July 19 question. These vectors were used in case (i) of part (a) above. The figure also shows, once more, the parallelogram construction of the vector sum a* + b*. In this construction, one joins the two vectors a* and b* tail-to-tail and then completes the parallelogram. The resultant a* + b* is represented by the arrow that points from the common tail end of a* and b* to the opposite corner of the parallelogram.
The last diagram in the figure shows the difference vector a* - b*. This vector is represented by the arrow from the tip of b* to the tip of a* if a* and b* are joined tail-to-tail. It is along the other diagonal of the parallelogram. The reason why this arrow represents a* - b* is that the equation (a* - b*) + b* = a* must be satisfied for the correct vector a* - b*. The diagram shows the head of b* joined to the tail of a* - b* and shows that the sum of these two vectors is indeed a*, represented by the arrow from the tail of b* to the tip of a* - b*.
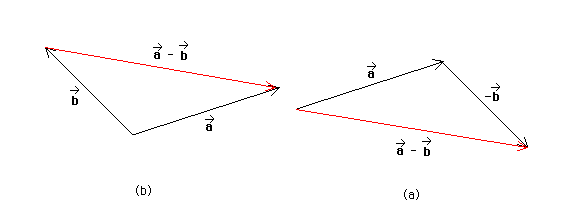
The following figure shows that the two constructions of the difference vector a* - b* presented in parts (a) and (b) above give the same result. The left diagram in the figure shows the tail-to-tail method for finding the difference, as used in part (b), while the right diagram shows the vector addition method via a* + (-b*), as used in part (a). The two triangles are congruent.
As an exercise, you should now try to find the difference a* - b* in cases (ii) and (iii) by using the tail-to-tail method of part (b). The answer should agree with that given in part (a).
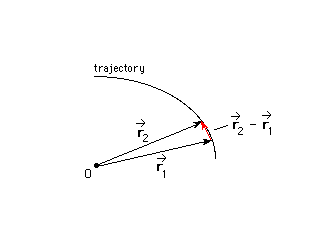
Important comment. The tail-to-tail method for finding the difference of two vectors is used when dealing with changes in a vector variable. Suppose, for example, a particle is moving along the trajectory shown in the following diagram. At two successive instants of time, 1 and 2, the particle is at the positions indicated by the position vectors r*1 and r*2. Then the change in the particle's position is defined as r*2 - r*1. This difference vector is indicated in red in the diagram. It points in the direction of the displacement of the particle during the time interval between instants 1 and 2, which is also the direction of the particle's average velocity during this interval.
The tail-to-tail method of finding the difference between two vectors portrays the intuitive significance of a difference. The difference between two vectors should be a measure of how different they are. Thus, finding a difference of two vectors is a kind of comparison between them. Now, if we want to compare two vectors (arrows), what is more natural than to draw them tail-to-tail and check how far their tips are apart. If the tips occupy the same spot, the vectors are identical. If the tips are close, as in the last diagram, the vectors are nearly identical so that their difference should be small. Thus, the arrow from the tip of one vector to that of the other is a good measure of what intuitively one might want to call the difference between the two vectors.
Return to Top of page.