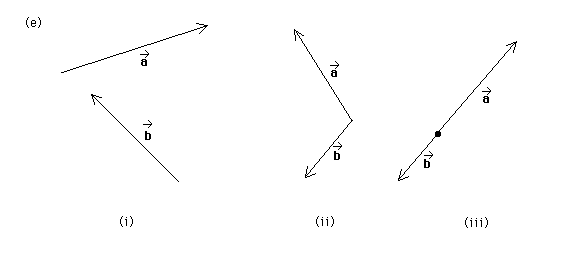
Question (a). Diagram (e) below shows three pairs of vectors a* and b*. For each case, find the sum of these two vectors. In the case of pair (iii), both vectors have their tail ends at the dot.

Answer. The following three diagrams, (f.i), (f.ii), and (f.iii), show the the sum a* + b* and how it is constructed, in each of the three cases. The two vectors are joined so that the head of the first vector, a*, is attached to the tail of the second vector, b*. The resultant, i.e., a* + b*, always points from the free (unattached) tail to the free (unattached) head. The resultant is shown in red.
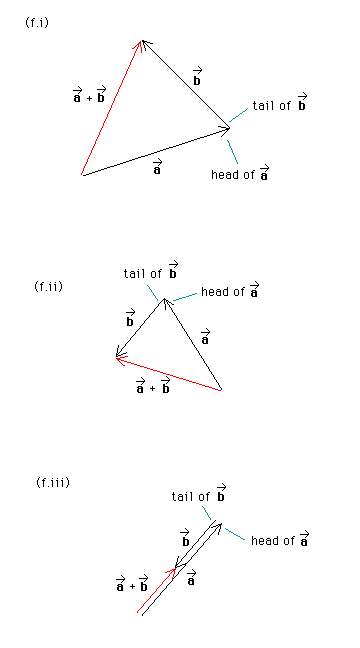
Note that in diagram (f.iii) the vectors are drawn side-by-side, rather than superimposed on each other. This way, one can see each vector more clearly. Remember that if the arrow representing a vector is shifted the vector represented by the arrow does not change as long as the length and direction of the arrow remain the same in the process.
Question (b). Show that vector addition is commutative, i.e., that a* + b* = b* + a*, for any two vectors a* and b*.
Answer. Diagrams (g.i) and (g.ii) show that the same vector results when the head of a* is joined to the tail of b* as when the head of b* is joined to the tail of a*. Thus, a* + b* = b* + a*.
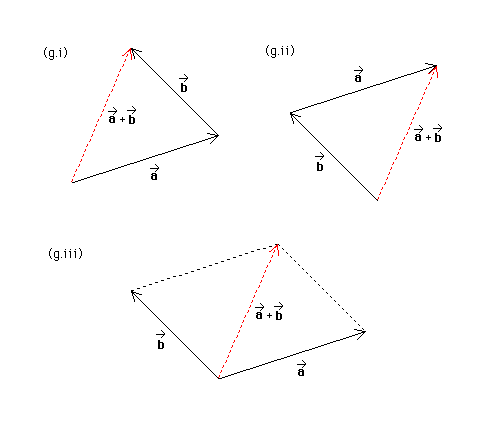
Note. Diagram (g.iii) shows that the resultant a* + b* is one of the two diagonals in a parallelogram whose sides consist of the two vectors a* and b*, namely, the diagonal that originates at the point where a* and b* are joined tail-to-tail. Thus we have a second method for finding the sum of two vectors: join the two vectors tail-to-tail, complete the parallelogram of which the two vectors form two sides, and then draw the diagonal from the point where the two vectors are joined tail-to-tail to the opposite corner of the parallelogram. This is called the parallelogram method of finding the sum of two vectors.
Question (c). Show that vector addition obeys the associative law, i.e., that (a* + b*) + c* = a* + (b* + c*).
Answer. Diagrams (h.i) and (h.ii) below illustrate the additions on the left-hand and right-hand sides, respectively, of the equation above. You can see that the green vector, which is the overall resultant, is the same in both cases.
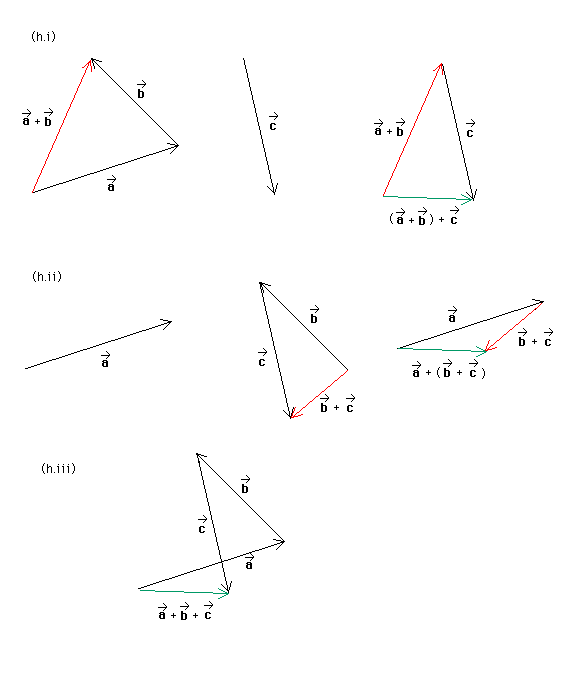
The reason why this is so is apparent from diagram (h.iii). When working out (a* + b*) + c* or a* + (b* + c*), one is effectively joining the three arrows in the manner illustrated in diagram (h.iii), i.e., head of a* to tail of b* and head of b* to tail of c*. This produces a unique resultant from the tail of a* to the head of c*.
Question (d). There exists a vector called the 'null vector' and denoted 0 (without an arrow above the symbol 0; this null vector is not, however, the same as the number 0; this notation is, therefore, not ideal). When the null vector is added to any given vector a* the result is again that vector, i.e., a* + 0 = a*. Find the arrow that would represent the null vector.
Answer. An arrow of zero length, i.e., a point, when added to any other arrow will not change that arrow. This is therefore the null vector. The null vector cannot be drawn on a diagram because a point is of zero size.
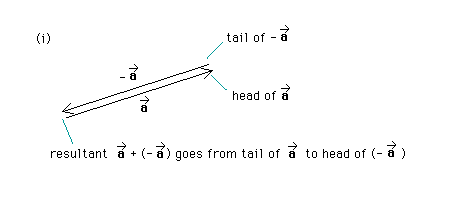
Question (e). For any given vector a*, there exists another vector denoted -a* such that a + (-a*) = 0. (Here, 0 denotes the null vector because the sum of two vectors is again a vector.) Draw a vector a* and find the corresponding vector -a*.
Answer. Diagram (i) below shows that when an arrow that has the same length as a* but opposite direction is added to a* the result will be the null vector because the tail of a* and the head of the reversed a* are at the same point (if a* and the reversed a* are drawn on top of each other, not side-by-side as in the diagram). Thus, -a* is obtained by reversing a*.