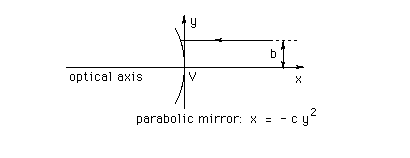
Suppose a parabolic mirror is oriented as in the diagram below, with rays parallel to the optical axis incident from the right. One such ray is shown.

Question. Prove that all rays incident on the mirror parallel to the optical axis are reflected so that they seem to be coming from one and the same point on the optical axis, which is again called the focal point. Find the distance between this focal point and the vertex of the mirror.

Answer. The following diagram is the same as the one above, with a few additions. Added is a ray incident on the mirror from the left, as in the June 28 question, that is the same distance away from the optical axis as the ray incident from the right. Added also are the two reflected rays (assuming the mirror reflects on both sides) and the normal to the mirror at the point where the two incident rays are reflected. This normal is shown as a stippled line.

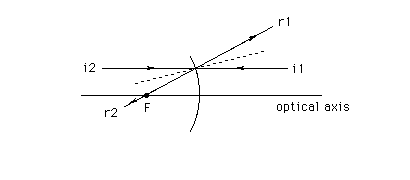
The diagram illustrates that ray i1 incident on the mirror from the right is reflected in such a manner that the reflected ray, r1, seems to be coming from point F on the optical axis. Point F is the focal point of the mirror already discussed in the answer to the June 28 question. It is the point through which all rays incident on the mirror from the left that are parallel to the optical axis will be reflected. One such pair of incident and reflected rays, rays i2 and r2, are shown in the diagram. The reason why all rays incident from the right parallel to the optical axis will be reflected so that the reflected rays seem to be coming from the focal point F will now be explained.

The angles formed between i1 and the normal and i2 and the normal are equal because these are opposing angles at the intersection of two straight lines. Therefore, the angles between r1 and the normal and r2 and the normal are equal because the law of reflection demands that the angles of incidence are equal to the angles of reflection. (Since the angles of incidence of the two rays i1 and i2 are equal, the corresponding angles of reflection of rays r1 and r2 must be equal as well.) This implies that rays r1 and r2 together form a straight line because r1 and r2 are turned relative to i1 and i2 by equal amounts. The fact that r1 and r2 form a single straight line means that r1 seems to be coming from point F since r2 goes through point F.

We know from the answer to the June 28 question that point F is a distance f = 1/(4c) away from the vertex of the parabola where c is the parameter in the equation for the parabola.