When learning a new subject, it is excellent practice to vary a question on the subject to which one already knows the answer.

Try this technique by varying the last question, the June 28 question. One variation is suggested below. In addition, try to make a variation of your own and work out the answer to your variation.

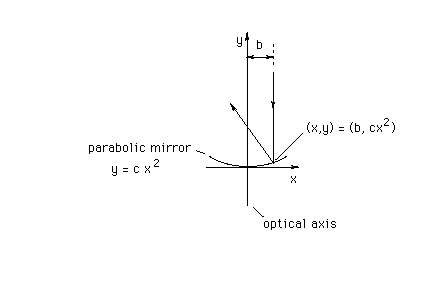
Question. Suppose a parabolic mirror is oriented as in the diagram below, i.e., turned 90 degrees relative to the orientation of the mirror in the June 28 question. You might ask yourself what equation would now describe the shape of the mirror. The answer is given in the diagram. Given this mirror, prove again that all rays incident on the mirror parallel to the optical axis are reflected so that they go through one and the same point on the optical axis, the focal point, which is a distance 1/(4c) away from the vertex of the mirror.

Answer. The following calculation parallels that done in the answer to the June 28 question. It would be useful for you to copy that solution on a piece of paper and compare each step to the corresponding step in the solution below.

Since the parabola above is turned by 90 degrees relative to the parabola in the June 28 question, and since otherwise nothing has changed (the incident ray still has a distance b from the optical axis), everything in the picture above including the direction of the reflected ray must be turned by 90 degrees relative to the corresponding elements in the diagram at the beginning of the Answer to the June 28 Question. This implies that the slope of the present reflected ray must be the negative reciprocal of that of the reflected ray in the June 28 case. Using the letter r to denote these slopes, with obvious subscripts to distinguish between the two cases, the two slopes are given by

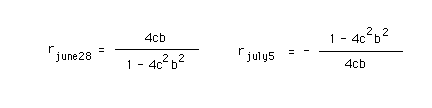
To find the y-coordinate of the point where the reflected ray intersects the y-axis, we write down the equation of the straight line of slope r that goes through the point where the incident ray hits the mirror. Then we set x = 0 in this equation and solve for y. These calculations are done below.

Note that the equation of the straight line written down here is the normal form of the equation, obtained by equating the ratio rise/run to the slope. The run is equal to the change in x-coordinate as one goes from the specific point x = b to the general point x while the rise is equal to the change in the y-coordinate as one goes from the y-value corresponding to x = b to the general point y.

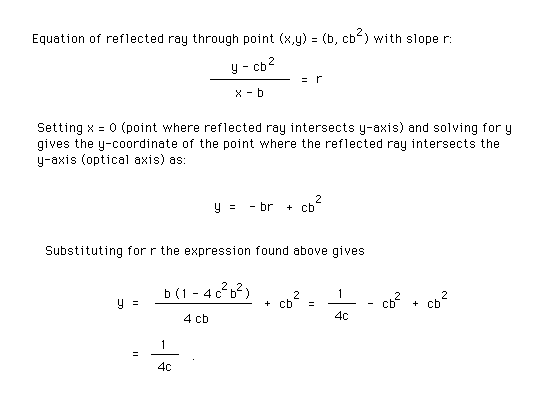
Again, the reflected ray intersects the optical axis at a distance f = 1/(4c) from the vertex of the mirror.