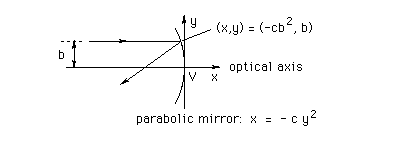
The diagram above shows a parabolic mirror and a ray incident on the mirror parallel to the optical axis. The optical axis is a line through the center (or vertex) V of the mirror such that the mirror is symmetrically positioned around this axis. The incident ray is a distance b away from the optical axis and is reflected by the mirror according to the law of reflection. (See the June 14 question.)

(a) Suppose the equation describing the shape of the mirror in terms of x and y coordinates is that given in the diagram above. Show that the point where the reflected ray intersects the optical axis is a distance f = 1/(4c) away from the vertex V of the mirror.

Hint. In order to deal with reflection by a curved mirror, you can pretend that the mirror acts like a plane mirror at the point of contact with the incident ray, where the slope of the plane mirror is equal to the slope of the curved mirror at this point. The slope of the parabolic mirror at a point whose y-coordinate is equal to b is equal to -1/(2cb).

Hint. You also will need the slope of the normal to the mirror at the point where the incident ray hits the mirror. If this slope is denoted by n and if the slope of the mirror at the point where the normal is taken is denoted by m, then n is given by n = -1/m. To see how the slope n of the normal is related to the slope of the reflected ray, see the second solution to Part (b) of the June 21 question.

Answer. The incident ray hits the mirror at y = b. According to the first hint, the slope m of he mirror at this value of y is given by m = -1/(2cb). With this value, the second hint gives us the slope n of the normal to the mirror at this point as n = 2cb. Note that this value is positive when b is positive. This makes sense when one looks at the diagram above. Also, the slope is proportional to b. This makes sense also if one thinks about how the normal changes as b changes.

As in the second solution to Part (b) of the June 21 question, the slope r of the reflected ray is then given in terms of n by

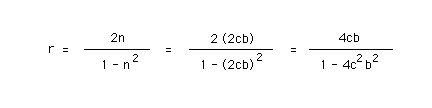
The preceding calculation applies to the situation (which is realized here) where the incident ray is parallel to the x-axis (optical axis) so that the angle formed between the reflected ray and the horizontal is twice that between the normal and the horizontal. (See the answer to the June 21 question.)

To find the x-coordinate of the point where the reflected ray intersects the x-axis, we write down the equation of the straight line of slope r that goes through the point where the incident ray hits the mirror. Then we set y = 0 in this equation and solve for x. These calculations are done below.

Note that the equation of the straight line written down here is the normal form of the equation, obtained by equating the ratio rise/run to the slope. The rise is equal to the change in y-coordinate as one goes from the specific point y = b to the general point y while the run is equal to the change in x-coordinate as one goes from the x-value corresponding to y = b to the general point x.

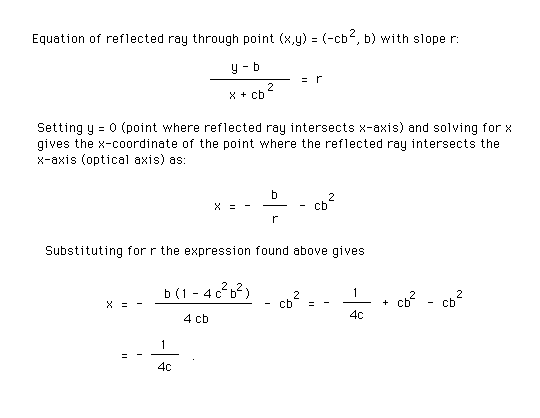
Thus, the reflected ray intersects the optical axis at a distance f = 1/(4c) from the vertex of the mirror. The minus sign in the result for x above indicates that the intersection point is to the left of the vertex, as it should be in the given set-up.