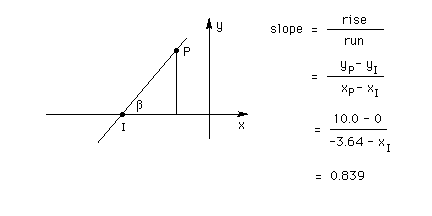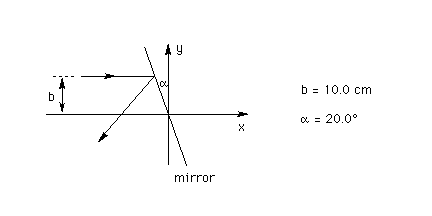
The physical situation is the same as in Part (a) of the June 14 question. See the diagram below and the June 14 question. Again, a horizontal ray of light is reflected by a plane mirror. The incident ray is a distance b = 10.0 cm away from the horizontal x-axis. The mirror is inclined relative to the vertical y-axis by the angle alpha = 20.0 degrees. The origin of the x,y coordinate system is placed at the point where the mirror intersects the x-axis.

Part (a). What are the x and y coordinates of the point at which the incident ray hits the mirror?
Answer.
Let the point where the incident ray strikes the mirror be denoted P. We already know the y-coordinate of point P. It is equal to 10.0 cm. We still need to find the x-coordinate. This requires that we calculate the length of the stippled line in the diagram below, i.e., the distance of point P from the y-axis.
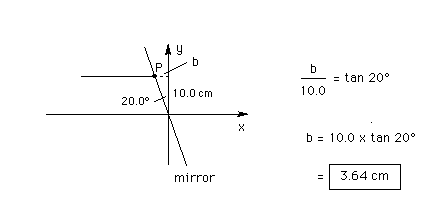
Let the distance of point P from the y-axis be denoted b. b is the length of the stippled line which is a side in the right-angle triangle containing part of the mirror as its hypothenuse and containing the 20-degree angle. This allows us to calculate b as indicated in the diagram above.
Since point P is to the left of the y-axis, its x-coordinate is negative and equal to -b. Thus, P has the coordinates (x,y) = (-3.64 cm, 10.0 cm).
Part (b). What is the slope of the reflected ray?
Answer.
The reflected ray forms an angle equal to 2x20 = 40 degrees with the horizontal axis. This result was derived in the answer to Part (a) of the June 14 question. You should review this derivation if necessary.
Therefore, the slope of the reflected ray is equal to tan (40 deg) = 0.839.
The diagram below illustrates why the slope of a straight line, rise/run, is equal to the tangent of the angle formed between the straight line and the horizontal axis.
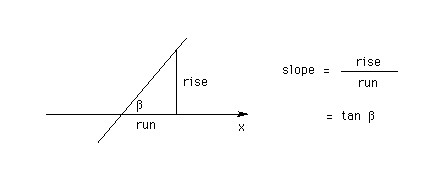
A second solution for finding the slope of the reflected ray will now be provided. It may seem more complicated than the first solution above, but it has the advantage of greater generality. E.g., it will be useful in solving next week's question.
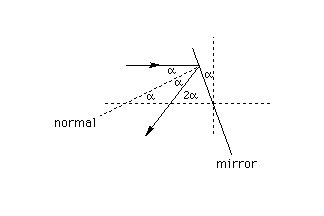
The diagram above shows angles that are equal to the angle alpha by which the mirror is inclined relative to the vertical. The diagram also shows that the angle between the reflected ray and the normal is equal to twice alpha. (Compare Diagrams (a1) and (a2) from the solution to part (a) of the June 14 question and the related explanation.)
Let the slope of the normal to the mirror be denoted by n. The diagram above shows that n = tan(alpha). Let the slope of the reflected ray be denoted by r. The diagram above shows that r = tan(2xalpha). Mathematical tables list all kinds of trigonometric identities, including the following one relating tan(2xalpha) to tan(alpha). With this identity, one can calculate r from n = tan(alpha) as shown below.
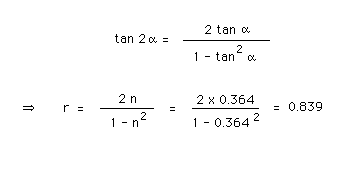
In the preceding calculation of r, we used n = tan(20 deg) = 0.364.
Part (c). At what distance from the origin of the x,y coordinate system does the reflected ray intersect the x-axis?
Answer.
One can calculate the x-coordinate of the point, I, where the reflected ray intersects the x-axis by expressing the slope of the ray in terms of the x and y coordinates of points P and I as indicated in the diagram below. Given the value of 0.839 of this slope from Part (b), one can solve the equation given in the diagram for the x-coordinate of the intersection point, x (subscript I), and obtains x (subscript I) = - 15.6 cm. Thus, this intersection point is 15.5 cm away from the origin.