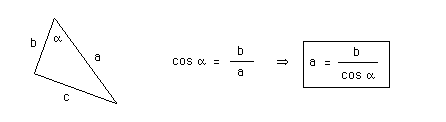
Question.

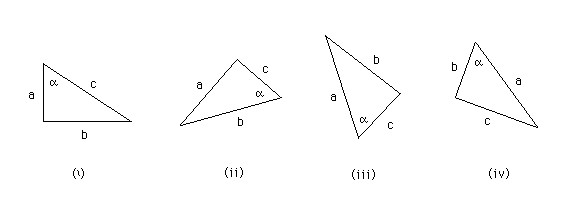
Each of the four triangles above contains a right angle. The three sides are labelled a, b, and c in no particular order. One of the two angles that is not a right angle is labeled by the Greek letter alpha.
The three most commonly used trigonometric functions are the sine, the cosine, and the tangent. These are the trig functions that you will find on all scientific pocket calculators.
For each of the four triangles (i) to (iv), express one of the three sides in terms of one of the other sides and an appropriate trig function evaluated for alpha. E.g., in the first row of the table below, you are asked to write down expressions for side a in terms of side b and angle alpha. Fill in all slots in the table.
Answer.
The table when completed should look as follows.
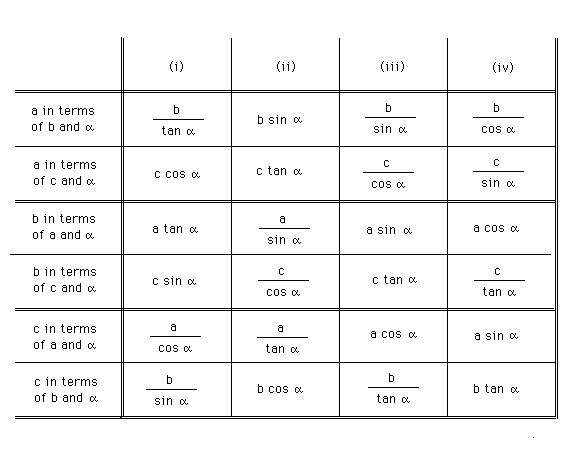
Explanation.
The sine, cosine, and tangent functions are equal to certain ratios of the sides in a right-angle triangle. These ratios are listed in the diagram below.
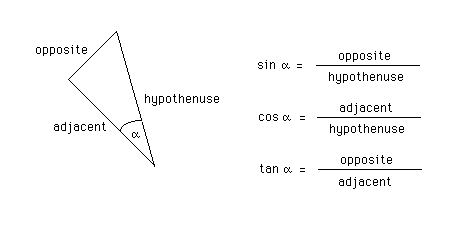
The hypothenuse is the side opposite to the right angle. The 'adjacent' to angle a is that side of the triangle that forms one of the two sides of the angle. (The hypothenuse forms the other side of the angle.) The 'opposite' to angle a is the side of the triangle opposite to the angle. In using trigonometric functions in a right-angle triangle, your first step should be to find the right angle and the hypothenuse, and then the adjacent and the opposite to a given angle in the triangle. If you are systematic in doing that, not too much else can go wrong, assuming you know the three equations for the sine, cosine, and tangent listed above. These equations must simply be memorized.
Three of the entries in the table will now be derived, one involving the sine, one the cosine, and one the tangent function. These are the entries in the first row of the table in columns (i), (ii), and (iv). The other entries are derived in analogous fashion.
a in terms of b and a for triangle (i):
c is the hypothenuse. a is the adjacent and b is the opposite to angle a. Thus,
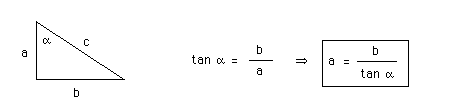
a in terms of b and a for triangle (ii):
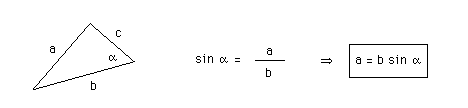
a in terms of b and a for triangle (iv):