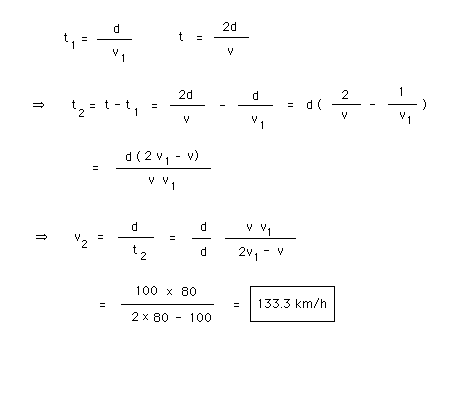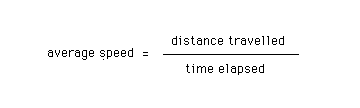
For this question you need to use the definition of average speed. The definition is as follows.
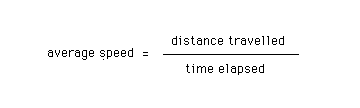
Suppose somebody drives from city A to city C via city B without stopping. The distance d from city A to city B is equal to the distance from city B to city C. Suppose also that the driver maintains an average speed of 80 km/h between cities A and B, but wants her average speed for the entire trip from city A to city C to be 100 km/h. What must be her average trip during the second part of the journey, from city B to city C?
This problem is not as easy as it may look. The answer is not 120 km/h. Do the problem in two ways.
Part (a) Assume that d = 40 km. Work out the time for the trip from A to B. Then work out the total travel time, given the overall average speed and total distance from A to C. From these two times you can find the travel time for the part of the trip from B to C. Now you can calculate the average speed for this part of the trip.
Answer. The average trip during the second part of the trip, from city B to city C, must be 133.3 km/h.
Explanation. If t1 denotes the time taken to go from A to B and v1 the average speed for this trip, then t1 = d/v1 = 40/80 = 0.5 h.
If t denotes the total travel time from A to C and v the overall average speed, then t = 2d/v = 80/100 = 0.8 h.
Therefore, the time t2 required to go from B to C must be t2 = t - t1 = 0.8 - 0.5 = 0.3 h.
This implies an average speed for the trip from B to C equal to v2 = d/t2 = 40/0.3 = 133.3 km/h.
Part (b) Now do the entire calculation in symbols, assuming no special value for the distance d. Show that the answer is independent of d.
Solution. Repeating the preceding calculation in symbols, step by step, gives