For this week's question, you need to have a bit of background on vectors. You may not have studied vectors before. In that case, look up vectors for a brief introductory lesson that will provide the necessary background including an explanation of the notation used here. You should also review the July 19 and August 2 questions.
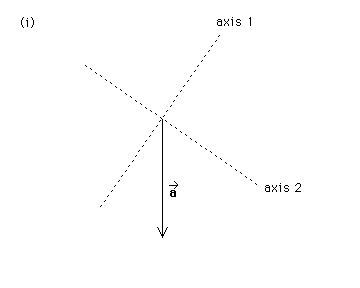
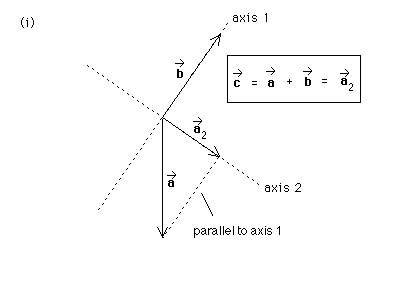
(a). The following diagram (i) shows a vector a* and two stippled axes. Find a vector b* along axis 1 such that c* = a* + b* is along axis 2.

Answer. We will decompose all vectors involved into their component vectors. The components will be taken along axes 1 and 2. This allows us to reduce the problem to finding the component vectors of b*. This is a simpler problem.
The component method is contained in the set of equations below.
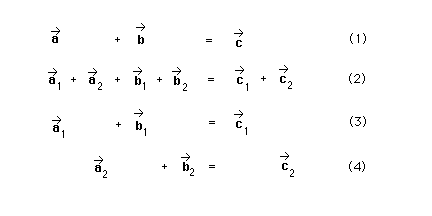
Equation (1) is the equation relating the three vectors we are dealing with in this problem: a*, b*, and c*. If we write a* as a sum of its components a1* and a2* and do the same for b* and c* and substitute all of this into equation (1), we obtain equation (2). Equation (2) can be satisfied by satisfying equations (3) and (4). (In fact, this is the only way to satisfy equation (2).) Equations (3) and (4) deal with either the 1-components or the 2-components alone and are therefore easy to deal with.
Let us now find b1* so that equation (3) is satisfied. Since we are told that c* is along axis 2, we know that c1* = 0. Thus, equation (3) reduces to a1* + b1* = 0. The following diagram shows a1* (obtained by drawing a line through the tip of a* parallel to axis 2; parallel projection of a* onto axis 1). The diagram also shows the vector b1* that added to a1* gives 0. It is a vector of equal magnitude and opposite direction to a1*.
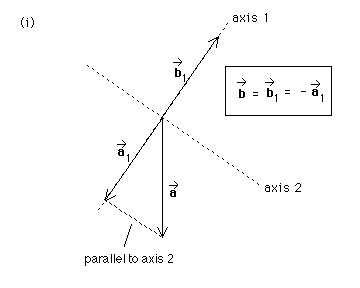
We don't need equation (4) at all for this part of the problem. Since we are told that b* is along axis 1, we know that b2* = 0. Thus, b* = b1* + b2* = b1* = -a1*.
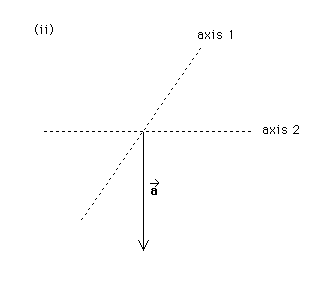
(b). The following diagram (ii) shows the same vector a* as in diagram (i) and two stippled axes, one of which is different from that in diagram (i). Again, find a vector b* along axis 1 such that c* = a* + b* is along axis 2.
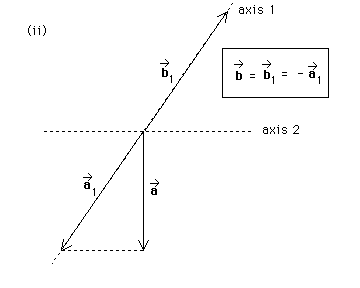
Answer. The solution of this part of the question is along exactly the same lines as that to part (a). The only difference is that the 1-component of a* is different because axis 2 is different in parts (a) and (b). Projecting parallel to axis 2 to find the 1-component of a* therefore gives different results. Compare the following diagram to that at the end of part (a).
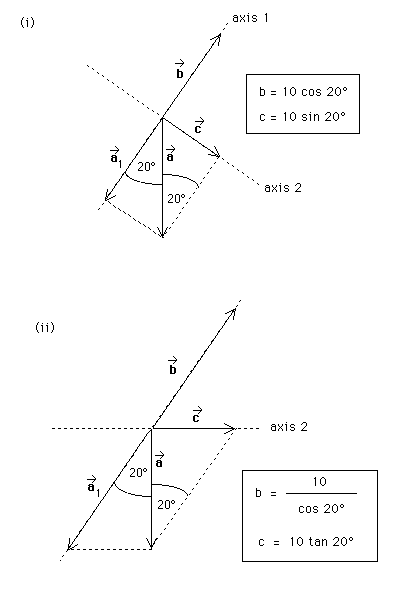
(c). Suppose the angle between vector a* and axis 1 is equal to 20 degrees. Suppose also that the length of an arrow represents the magnitude of the corresponding vector. Take the magnitude a of vector a* to be equal to 10. Calculate the magnitudes of vectors b* and c* = a* + b* in cases (i) and (ii). Write your answers in the form of equations using the appropriate symbols.
Answer. In order to determine the vector c*, we need equation (4) above. Since c* is known to be along axis 2, its 1-component is equal to zero. Thus we need to determine only its 2-component, by using equation (4). Since the 2-component of b* is zero, we have c* = a2*. The following two diagrams illustrate how to construct a2* in cases (i) and (ii).
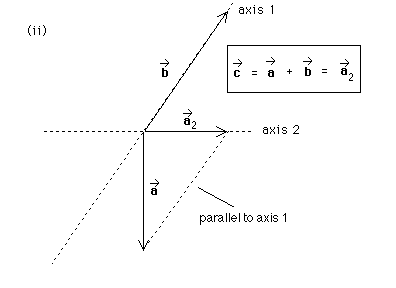
The following two diagrams summarize the previous results for cases (i) and (ii) and also show which angles are equal to 20 degrees. Remember that b = |a1*|. (The notation for the magnitude of vector b is b* and for the magnitude of a1* is |a1*|.) Using a = 10 and the trigonometry of right-angle triangles, reviewed in the June 7, 1996 Question, we obtain the results for b and c that are indicated in the boxed equations in the diagrams below.