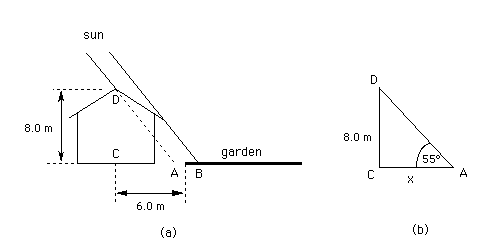
(a) A gardener lays out his garden on the north side of his house. The ridge of the house is oriented east-west and is 8.0 m above the level of the garden. The part of the garden closest to the house is 6.0 m away in the horizontal direction from the ridge of the house.
Will all of the garden be in the sun when the sun is in the south and 55 degrees above the horizon?
Answer.
Yes, if it is indeed the ridge and not the edge of the roof of the house that is throwing the shadow.
Explanation.
Diagram (a) below shows two rays from the sun, hitting the ground at points A and B, respectively. The ray hitting the ground at A is shown stippled. This ray forms the edge of the shadow assuming the roof is steep enough to not obstruct the ray so that the ray will actually reach the ground. (This is not the case if the roof is as illustrated in Diagram (a).)
For the situation where the ray DA determines the shadow's edge, the relevant triangle is redrawn in Diagram (b). The corners A, D, and C of this triangle correspond to the points labeled A, D, and C in Diagram (a).

Trigonometry allows us to calculate the distance x from point C directly below the ridge to point A at the edge of the shadow when the sun's ray DA forms a 55 degree angle with the horizontal. The calculation is as follows.
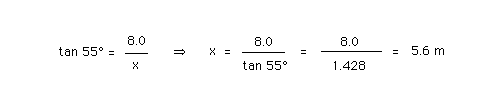
Since 5.6 m is less than the distance from C to the beginning of the garden, which is 6.0 m, all of the garden will be in the sun.
If the roof of the house is inclined by less than 55 degrees relative to the horizontal, it will be the edge of the roof that is throwing the shadow, as illustrated by ray DB in Diagram (a). In this case, a part of the garden may well be in the shade when the sun is 55 degrees high in the sky.
(b) How high in the sky, i.e., how many degrees above the horizon, will the sun be at noon on the longest day of the year, June 21st, in Calgary?
Data: The latitude of Calgary is 51.3 degrees. The earth rotates once per day around an axis that is inclined by 23.5 degrees relative to the plane in which the earth orbits around the sun.
Answer.
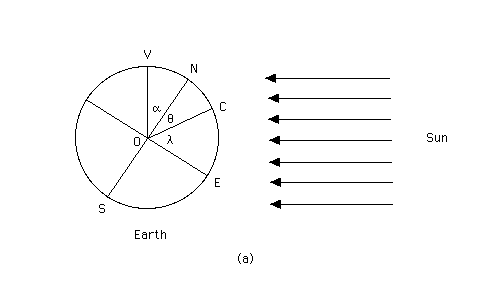
The sun will be 62.5 degrees high in the sky. This value is equal to the colatitude of Calgary plus the tilt angle of the earth's axis. The colatitude is the angle between the earth's axis ON and the radius OC from the earth's center to Calgary, which is at point C. (See Diagram (a) below.) Calgary's colatitude is equal to 90 - 51 = 39 degrees. Thus, the elevation of the sun above the horizon at noon on the longest day of the year is 39 + 23.5 = 62.5 degrees.
Explanation.
Diagram (a) shows the earth on the longest day of the year at noontime in Calgary and the (very nearly) parallel light rays from the sun to the earth. On this day, the earth's axis is positioned so that its upper half, ON, is tilted directly towards the sun, and its lower half, OS, is tilted directly away from the sun. N and S are the earth's north and south poles, respectively. At noon, Calgary is at point C, directly facing the sun. E is the point on the earth's equator facing the sun.
The latitude of Calgary is equal to the angle COE and is denoted by the Greek letter lambda in Diagram (a). The colatitude of Calgary is equal to the angle CON and is denoted by the Greek letter theta in Diagram (a). The tilt angle of the earth's axis is the angle VON and is denoted by the Greek letter alpha in Diagram (a). Lines ON and OE form a 90-degree angle between them, which implies that the latitude and the colatitude add up to 90 degrees.
We need another angle, namely, the angle between the radius OC and the horizontal radius OH. This angle is denoted by the Greek letter beta in Diagram (b) below. The equatorial radius OE is tilted relative to the horizontal radius OH by the same angle alpha by which the polar radius ON is tilted relative to the vertical radius OV. Therefore the latitude lambda of Calgary, which is the angle COE, is equal to alpha + beta.
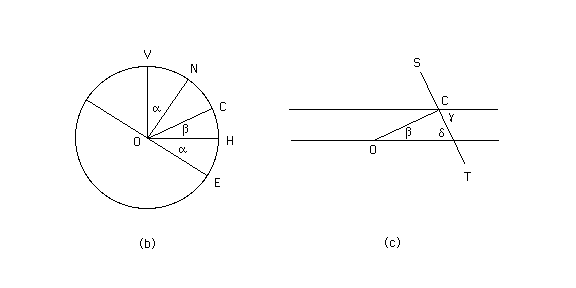
Finally, we come to the angle that the question is asking for, which is the angle between the direction of the incoming sunlight and the horizontal plane at Calgary. This is the angle denoted by the Greek letter gamma in Diagram (c) above. The line ST lies in the plane that is tangential to the earth's surface at Calgary, i.e., at point C. This is the plane that Calgarians would consider to be horizontal. (It does not look horizontal in the diagram.) It is perpendicular to the radius OC. ST intersects the continuation of the horizontal radius OH, and the angle between these two lines is denoted by the Greek letter delta in Diagram (c).
By a theorem from geometry, angles delta and gamma are equal. This theorem says that the opposing angles (delta and gamma) formed at the intersections of a straight line (ST) with two parallel lines (the lines through C and O) are equal.
Since beta and delta are angles in a right-angle triangle, they add up to 90 degrees. Therefore, we can obtain gamma as follows:
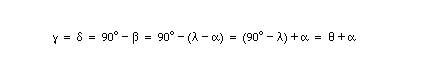
In words, the angle of elevation of the sun above the horizon at noon on the longest day of the year is equal to the sum of the colatitude of Calgary and the tilt angle of the earth's axis.