In the following Activities, it is assumed that the applet's slider settings are the default settings except when there are instructions to the contrary. In particular, make sure that the speed v of the mass point is constant, i.e., that the dv/dt-slider is set to 0.

Activities

1. Display the acceleration of the mass point such that the vector has its tail end at the mass point (select "acceleration at particle" in the Vector Panel). Display no other vectors. Make sure the applet is in the Continuous mode. Display the position trace (Trace P), but not the velocity trace (Trace V). Set the initial speed of the mass point to v(0) = 0.25 m/s. Since the speed is constant, the speed will be equal to 0.25 m/s at all times during the motion. This value for the speed will be used in all of the following Activities.

   Play the motion, and Pause it at several places. Make a drawing showing the path of the mass point and the acceleration vector at different points of the path.

   In a sentence, describe the direction of the acceleration vector of the mass point at different points of the path. Adjectives used to describe this direction are "radial" and "centripetal". Are they appropriate?

2. Activities 2 to 5 are intended to explain why the acceleration in uniform circular motion has a radial direction. The explanation is based on the fact that the relationship of acceleration to velocity is analogous to the relationship of velocity to position. Compare the definitions of the two quantities:

   Acceleration is the time-rate-of-change of velocity while velocity is the time-rate-of-change of position.

   Let's review the relationship between velocity and position.

   Reset the applet. Set the initial speed to v(0) = 0.25 m/s, and display the two vectors that in the Vector Panel are called "position" and "velocity at particle".

   Play the motion. (For detailed suggestions on what to observe, close this Activities window and go to Activities on Velocity.) Can you confirm the following general statement?

   The velocity vector at a given instant points in the direction in which the tip of the position vector is moving at that instant, which is the direction of the tangent to the mass point's path at that instant.

3. Continuing from Activity 2, click Rewind, make sure the applet is in the Continuous mode, and display a second velocity vector, the one called "velocity at origin" in the Vector Panel, in addition to the velocity-at-particle and position vectors already on display. The new velocity vector has its tail end fixed at the origin and in that sense is like the position vector which has its tail end fixed at the origin also. Notice that the two magenta velocity vectors are identical in magnitude and direction. They differ only in location. Vectors can always be drawn wherever it is convenient.

   Play the motion, and observe how the two velocity vectors remain identical throughout the motion.

   Click Rewind, and display the velocity trace (Trace V). Then Play the motion. Observe that the trace (magenta) of the tip of the velocity-at-origin vector is circular also, like that of the tip of the position vector. However, imagine the velocity vector and its trace to be in a differenct space, called velocity space, shown superimposed on position space, the space in which the position vector exists. The radius of the circular trace in velocity space is equal to the magnitude of the velocity vector, which is v = 0.25 m/s.

4. Continuing from Activity 3, click Rewind. Observe that the velocity-at-particle vector points in the direction of motion of the tip of the position vector. Draw the configuration of these two vectors and the position trace in your Notebook. Then try to draw an acceleration vector that has its tail end attached to the tip of the velocity-at-origin vector and that points in the direction of motion of the tip of this velocity vector.

   Check your prediction of the direction of the acceleration vector by selecting "acceleration at velocity" in the Vector Panel, and Play the motion.

   To focus on just the relationship of the acceleration and velocity-at-origin vectors, hide the other two vectors and the position trace by deselecting "position" and "velocity at particle" in the Vector Panel and deselecting the Trace-P button. Can you confirm the following general statement?

   The acceleration vector at a given instant points in the direction in which the tip of the velocity-at-origin vector is moving at that instant, which is the direction of the tangent to the velocity trace at that instant.

With the position and velocity-at-particle vectors still hidden, display a second copy of the acceleration vector, the one called "acceleration at particle" in the Vector Panel. This is the vector displayed in Activity 1 whose direction was called "radial" or "centripetal".

5. Here is another way to demonstrate that the acceleration is in the radial direction based on the analogy between the acceleration-velocity and velocity-position relationships.

   Continuing from Activity 4, select "position", "velocity at origin", and "acceleration at origin" from the Vector Panel, but no other vectors. Hide the position and velocity traces. Thus, only three different-colored vectors should remain on the screen, all of them with their tail ends at the origin.

   Play the motion. Since the velocity vector is 90^o ahead of the position vector, the acceleration vector should be 90^o ahead of the velocity vector. As the applet shows, this makes the direction of the acceleration vector radial and opposite to the position vector.

   By the way, when the acceleration vector is drawn with its tail end attached to the origin, can its direction still be called "centripetal" which is derived from Latin and means "center seeking"? Referring to the direction as "radial" is still appropriate.

   Activities 2 to 5 are based on the analogy between the acceleration-velocity relationship to the velocity-position relationship. Using this analogy, the activities show that the direction of the acceleration in uniform circular motion is radial.

6. The remaining three Activities are designed to provide an understanding of acceleration in uniform circular motion that is based solely on the definition of acceleration as time-rate-of-change of velocity.

   Reset the applet, set it to the Incremental mode, and set the time step to Dt = 0.50 s. Display only the velocity-at-origin and acceleration-at-velocity vectors. Display the velocity trace (Trace V), but not the path of the particle (Trace P).

   Use the Step button to take one step into the motion. Make a drawing of the velocity vectors _i and _f at the beginning and end of the time step, the change in velocity vector D during the time step, and the acceleration vector 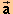_i at the beginning of the time step. Estimate the angle between the change in velocity and acceleration vectors.

   Click Rewind, reduce the time step to Dt = 0.25 s, and again take the first step into the motion. Again, draw all vectors and estimate the angle between the initial acceleration vector and the change in velocity vector. Compare the situation to that for Dt = 0.50 s. Can you see that the direction of D approaches that of 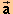_i as Dt decreases?

   Click Rewind, and repeat these observations once more for a time step Dt = 0.10 s.

   Acceleration is defined as the limit of the ratio D/Dt as Dt approaches 0. As Dt approaches 0, does the direction of D/Dt, which is the same as that of D, approach the direction of the acceleration at the beginning of the time interval?

   The change in velocity D forms a cord of the circular velocity trace. Do you observe that as Dt approaches 0 the direction of the cord approaches that of the tangent to the path at the initial point of the given time step?

   Can you confirm that the acceleration vector at a given instant points in the direction in which the tip of the velocity vector is moving at that instant, which is the direction of the tangent to the velocity trace at that instant?

7. This activity is a repeat of Activity 6 with numbers.

   Continuing from Activity 6, click Rewind, change the step size back to Dt = 0.50 s, and display the Data box. Make sure the applet is still in the Incremental mode and that no other settings have changed.

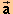   Take one step into the motion. Record the values of D and Dt, and work out the ratio D/Dt in terms of its x,y scalar components. Compare this ratio to the initial acceleration _i.

   Using the x,y scalar components of D/Dt worked out above and the x,y scalar components of 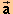_i listed in the Data box, draw the two vectors D/Dt and 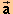_i. Draw them with their tail ends joined for better comparison. For better accuracy, you may want to draw the vectors on graph paper.

   As in Activity 6, repeat this with time steps equal to 0.25 s and 0.10 s.

   Does D/Dt approach 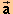_i as the size of the time step decreases?

   The applet will let you choose time steps smaller than Dt = 0.10 s, but the values of D/Dt will become unreliable as the time step becomes too small because of a loss of significant figures. This is evident visually as well because the change in velocity vector D becomes hard to recognize.

8. Repeat Activities 6 and 7 at a different time point. E.g., after clicking Rewind, drag the mass point to a point with phase d = 1 rad. (d is the first item in the Data box). Use this point as the initial point for the time step.