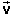 /dt in Eq.(1) for the acceleration
/dt in Eq.(1) for the acceleration 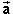 as a ratio of two
infinitesimal quantities and solving for d
as a ratio of two
infinitesimal quantities and solving for d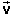 gives
gives
The acceleration of a mass point is defined on Page 1. Two sets of basic equations for the products of acceleration and time elapsed and acceleration and displacement are stated below. The numbering of equations continues from Page 1.
Acceleration Multiplied By Time Elapsed
Treating the symbol d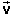 /dt in Eq.(1) for the acceleration
/dt in Eq.(1) for the acceleration 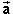 as a ratio of two
infinitesimal quantities and solving for d
as a ratio of two
infinitesimal quantities and solving for d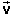 gives
gives
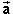 dt =
d
dt =
d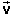 .
. ![]() (3)
(3)
Eq.(3) applies to an infinitesimal time interval of duration
dt. It equates the product of the particle's acceleration
and the infinitesimal time elapsed dt to the change
d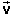 in the
particle's velocity during the elapsed time interval.
in the
particle's velocity during the elapsed time interval.
To find the change Δ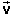 in the particle's velocity during a
finite time interval of duration Δt, one has to sum the terms
in the particle's velocity during a
finite time interval of duration Δt, one has to sum the terms 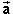 dt for all
infinitely many infinitesimal time intervals that make up Δt. A sum over infinitesimals is called
an integral. Calculus provides rules for working out
integrals. One needs to know how the acceleration depends on time
in order to work out the integral for a specific case.
dt for all
infinitely many infinitesimal time intervals that make up Δt. A sum over infinitesimals is called
an integral. Calculus provides rules for working out
integrals. One needs to know how the acceleration depends on time
in order to work out the integral for a specific case.
For the special case in which the acceleration is constant during
a time interval of finite duration Δt, the integral (sum) of the 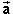 dt terms can be done without
knowing the rules of calculus. The result is
dt terms can be done without
knowing the rules of calculus. The result is
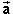 Δt = Δ
Δt = Δ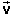 ,
, ![]() if
if 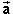 = const.
= const.![]() (4)
(4)
Acceleration Multiplied by Displacement
The infinitesimal displacement d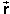 of a particle during an infinitesimal
time interval is a vector quantity. Multiplying the acceleration of
a particle by the particle's infinitesimal displacement means using
the scalar product. The result is:
of a particle during an infinitesimal
time interval is a vector quantity. Multiplying the acceleration of
a particle by the particle's infinitesimal displacement means using
the scalar product. The result is:
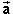
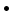 d
d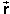 = (1/2)dv2
= (1/2)dv2
![]() or
or ![]() 2
2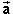
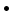 d
d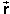 = dv2
= dv2 ![]() (5)
(5)
where v is the particle's speed.
For the special case in which the acceleration is constant during
a finite time interval while the particle undergoes the finite
displacement Δ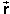 , the terms
, the terms 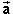
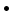 d
d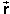 can be summed (integrated) without knowing any
formal rules of calculus. The result is:
can be summed (integrated) without knowing any
formal rules of calculus. The result is:
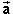
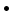 Δ
Δ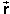 = (1/2)Δv2
= (1/2)Δv2 ![]() or
or![]() 2
2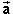
 Δ
Δ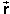 = Δv2,
= Δv2,![]() if
if 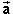 = const.
= const.![]() (6)
(6)
For one-dimensional motion along an x-axis, Eqs.(5) and (6) reduce to the following Eqs.(7) and (8), respectively.
2axdx = dv2![]() (7)
(7)
2axΔx = Δv2,![]() if
if 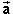 = const.
= const.![]() (8)
(8)
For a derivation of Eqs.(5) and (7), see Acceleration/Instantaneous/Explain It.