Lesson 1 - Conservation of Momentum in 2D Collisions

The Collisions 2D applet simulates elastic and inelastic two-dimensional collisions in both the lab and centre of mass frames.

Prerequisites

Students should have a basic understanding of vectors and vector components and a working knowledge of trigonometry. Students should be familiar with the Law of Conservation of Momentum and how to set-up and solve collision questions.

Learning Outcomes

In this lesson you will learn about momentum and two dimensional collisions. Students will be able to define and calculate the momentum of an object. Students will also be able to show that momentum is conserved in 2D collisions. As well, students will be able to analyse and predict the outcome of collisions using conservation laws.

Instructions

Students should know how the applet functions, as described in Help and ShowMe. The applet should be open. The step-by-step instructions on this page are to be done in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited.

Contents

Background

In previous lessons, you learned about momentum and the law of conservation of momentum in one-dimensions. In this lesson, you will examine momentum in two-dimensional situations. As review, complete the following questions about momentum and collisions.

  1. What is momentum and how is it calculated?



  2. What is the momentum of:
    1. a 300 kg car travelling east at 115 km/hr?


    2. a 500 kg truck waiting at a stoplight?


  3. What is the Law of Conservation of Momentum?



  4. Object A has a mass of 3.0 kg. It is travelling to the right with a speed of 4.75 m/s. Suddenly, it collides in a head-on, perfectly elastic collision with object B, which is at rest and has a mass of 5.0 kg. After the collision, object B is now moving to the right at 3.56 m/s. In what direction and with what speed is object A now travelling?

Momentum and Vector Components

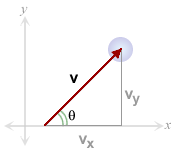Momentum is "mass in motion", or a measure of how much motion an object has. Algebraically, momentum is defined as the product of an object's mass and velocity, . Momentum is a vector - the direction of the momentum matters.

Any vector can be resolved into components. Generally, we resolve vectors into horizontal (x) and vertical (y) components. The diagram to the right shows a vector, v, resolved into its x and y components.

Using the diagram to the right and some basic trigonometric identities, answer the following questions.

  1. What is the expression that gives vx as a function of v and q?



  2. What is the expression that gives vy as a function of v and q?



  3. Write a general expression for v, if both vx and vy are known.



  4. If both vx and vy are known, what is the general expression for q?



 

2D Collisions and Conservation of momentum

In previous lessons you have already seen that the total momentum of a system is conserved during a collision. But in those lessons, you were only looking at one-dimensional collisions. Let's now investigate how momentum is conserved in two-dimensional collisions. Use the applet to help you answer the following questions. Un-check Show CM and Show CM Frame.

  1. Perform five different collisions and complete the following tables. To generate a new collision, either set your own conditions or press the new button ( ). To view the collision information, press the data button ( ).

    Collision 1
    Object
    mass
    (kg)
    vinitial
    (m/s)
    vfinal
    (m/s)
    D v
    (m/s)
    pinitial
    (kg·m/s)
    pfinal
    (kg·m/s)
    D p
    (kg·m/s)
    Blue
     
     
     
     
     
     
     
    Green
     
     
     
     
     
     
     

 

Analysing Collisions

In the previous section you discovered that the total momentum of a system is conserved, as long as there are no external forces acting on a system. Let's use the conservation of momentum to analyse the following collisions. When solving multi-step questions, it is useful to follow a four-step method:

Let's do an example question together:

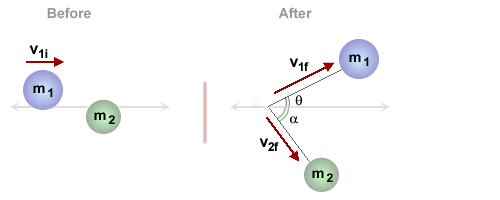
Example:

An 8.0 kg mass collides elastically with a 5.0 kg mass that is at rest. Initially, the 8.0 kg mass was travelling to the right at 4.5 m/s. After the collision, it is moving with a speed of 3.65 m/s and at an angle of 27° to its original direction. What is the final speed and direction of motion for the 5.0 kg mass?

Solution:

  1. Plan-it: Initially, the 8.0 kg mass (mass 1) moves to the right and the 5.0 kg mass (mass 2) is at rest. Thus, the total momentum is in the x-direction (to the right). After the collision, mass 1 travels at an angle of 27° to its original direction of motion - it now has momentum in the y-direction and the x-direction. For momentum to be conserved, mass 2 must have momentum in the x and y directions.


  2. Set-it-up: Motion to the right is positive. Following convention, angles are measured counterclockwise, from the horizontal. Our unknown information is the final velocity of mass 2 and its direction of motion, a. Furthermore, since this is a 2D problem, we should include the x and y components of the velocities:

    We will use the Law of Conservation of Momentum to solve this question. Since momentum is conserved in both the x and y directions, we can set up two sets of equations, one to solve for v2fx and v2fy:

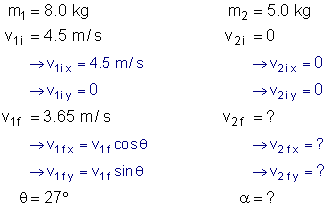
    Conservation of momentum in the x-direction: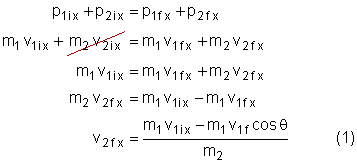
    		 Conservation of momentum in the y-direction: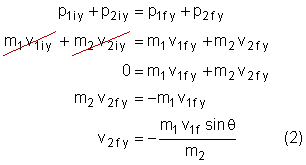

  3. Solve-it: Now we substitute known values into equations 1 and 2:

    Mass 2's final velocity in the x-direction: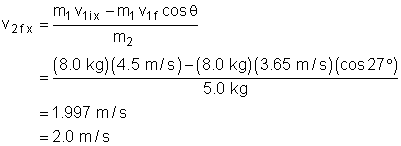
    		 Mass 2's final velocity in the y-direction: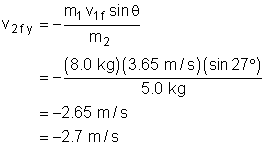

    Once we know the final velocity in the x and y directions, we can easily determine the final velocity and direction of motion for mass 2. Remember, do not round off during your calculations - only at the end.

    Mass 2's final velocity: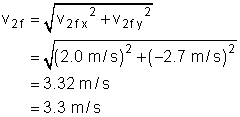
    		 Direction of motion: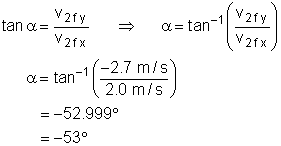

  4. Think-About-It: Our answer seems to make sense - we know that mass 2 has to move to the right and down in order to conserve momentum. Furthermore, this answer can be verified with the applet (check it yourself!).

Now it's your turn! Solve each question using the four-step method. Use the applet to help visualise the collisions and also to check your answers. Remember that to set the scatter angle, you must actually adjust the impact parameter (while viewing the data box, adjust the impact parameter until the scatter angle is correct).

 

Summary

In this lesson you looked at collision that occur in two-dimensions. You saw that the total momentum of a system is conserved during a collision. Moreover, the total momentum in the x-direction and in the y-direction is also conserved during a collision. The key points you looked at are: