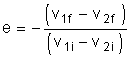Lesson 2 - Elasticity and Conservation of Kinetic Energy

The Collisions 1D applet simulates elastic and inelastic one-dimensional collisions in both the lab and centre of mass frames.

Prerequisites

Students should have a basic understanding of vector and scalar quantities, and should be able to define kinetic energy qualitatively and algebraically. Students should also have an understanding of conservation of momentum and equation manipulation.

Learning Outcomes

In this lesson you will learn about the elasticity of a collision and the conservation of kinetic energy. Students will be able to define, compare and contrast elastic and inelastic collisions. Students will also be able to compare vector and scalar conservation laws and predict the results of a collision using these conservation laws.

Instructions

Students should know how the applet functions, as described in Help and ShowMe. The applet should be open. The step-by-step instructions on this page are to be done in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited.

Contents

Background

In a previous lesson you looked at something called momentum. As you remember, momentum is a vector. In this lesson, however, we will be focusing on a scalar quantity - kinetic energy. We will investigate the role of kinetic energy in collisions and decide whether it is also conserved. But before we look at collisions and kinetic energy, let's review momentum and kinetic energy.

1. In one or two sentences, describe what momentum is. How is momentum calculated?
   
   
   
   
2. Explain the Law of Conservation of Momentum.
   
   
   
   
3. What is the difference between potential and kinetic energy?
   
   
   
   
4. How is kinetic energy calculated?
   
   
   
   
5. Two bumper cars, each with a mass of 50 kg are headed toward each other with speeds of 6 km/hr.
   1. What is the momentum of each car? Do the cars have the same momentum?
      
      
      
   2. What is the total momentum of the system?
      
      
      
   3. What is the kinetic energy of each car? Do the cars have the same kinetic energy?
      
      
      
   4. What is the total kinetic energy of the system?

1D Collisions and Kinetic Energy

Kinetic energy is energy of motion. Any object that is moving not only has momentum, but also has kinetic energy. In previous lessons, you discovered that the total momentum of a closed, isolated system is conserved during a collision. But, what about kinetic energy - is it also conserved? Use the applet to help you answer the following questions. On the applet, un-check Show CM and Show CM Frame.

6. Using the applet, investigate five different collisions between the same objects and complete the tables below. For each collision, you are verifying that momentum is conserved and checking to see if kinetic energy is conserved. To view the collision information, press the data button ( ). To set up the collisions, follow these steps:
   • press the options buttons
     • make sure that under Collision Settings, e is set to random
     • under Particle Settings, select input ( ) for both particles and give them the same mass
   • pressing the new button ( ) will generate collisions with new e values, but will maintain the masses that you have specified.
   • adjust the velocity slider to vary the initial velocity of the blue mass.
     
     

   Do not worry about what e represents - this will be discussed later. The value of e will be listed with the other applet information.
   

   Collision 1           e = _____
   Object	mass (kg)	vinitial (m/s)	vfinal (m/s)	pinitial (kg·m/s)	pfinal (kg·m/s)	Ek initial (J)	Ek final (J)
   Blue
   Green
   Total	---	---	---

   
   

   Collision 2          e = _____
   Object	mass (kg)	vinitial (m/s)	vfinal (m/s)	pinitial (kg·m/s)	pfinal (kg·m/s)	Ek initial (J)	Ek final (J)
   Blue
   Green
   Total	---	---	---

   
   

   Collision 3          e = _____
   Object	mass (kg)	vinitial (m/s)	vfinal (m/s)	pinitial (kg·m/s)	pfinal (kg·m/s)	Ek initial (J)	Ek final (J)
   Blue
   Green
   Total	---	---	---

   
   

   Collision 4          e = _____
   Object	mass (kg)	vinitial (m/s)	vfinal (m/s)	pinitial (kg·m/s)	pfinal (kg·m/s)	Ek initial (J)	Ek final (J)
   Blue
   Green
   Total	---	---	---

   
   
   

   Collision 5          e = _____
   Object	mass (kg)	vinitial (m/s)	vfinal (m/s)	pinitial (kg·m/s)	pfinal (kg·m/s)	Ek initial (J)	Ek final (J)
   Blue
   Green
   Total	---	---	---

   
   
   
7. Now, look at the information in your tables.
   1. Is momentum conserved in each collision?
      
      
      
      
   2. Is kinetic energy conserved in each collision?
      
      

In a collision, momentum is always conserved, but not kinetic energy. Sometimes, the kinetic energy is nearly conserved and in other collisions, it is hardly conserved at all. What is going on? To answer this question, we must consider is happening to the objects during a collision.

Elastic and Inelastic Collisions

During a collision, energy changes form. As objects interact and collide, they change shape and are distorted. As this occurs, the kinetic energy of the colliding bodies is converted into potential energy, or dissipated as sound or heat. The extent to which energy is converted back to kinetic energy after the collision determines the "elasticity" of the collision.

There is a spectrum of elasticity: collisions can range from being perfectly elastic to perfectly inelastic. As collisions become more and more inelastic, less and less kinetic energy is conserved.

Perfectly Elastic Collisions In a perfectly elastic collision, the total kinetic energy of the system is conserved. Perfectly elastic collisions generally occur only at the subatomic level Inelastic Collisions In an inelastic collision, some kinetic energy is lost, generally as sound or thermal energy. This is a broad range and most collisions fall within this class. Perfectly Inelastic Collisions: In a perfectly inelastic collision (also called completely inelastic), the colliding objects stick together upon impact. There is the greatest loss of kinetic energy in this type of collision.

8. Imagine throwing a super-ball (a very bouncy ball) against the wall.
   1. Describe the shape of the ball before, during and after the collision.
      
      
      
      
   2. Describe what happens to the kinetic energy of the ball during the interaction. Is the kinetic energy of the ball conserved? If not, what happened to it?
      
      
      
      
      
9. Now, imagine throwing a blob of playdough at the wall.
   1. Describe the shape of the blob before, during and after the collision.
      
      
      
      
   2. Describe what happens to the kinetic energy of the blob during the interaction. Is the kinetic energy of the blob conserved? If not, what happened to it?
      
      
      
      

Now that we have discussed the idea of elasticity, let's return to the collisions you performed earlier. This time, we will look at what e represents.

10. For each of your collisions, calculate the percentage of kinetic energy lost during the collision and fill in the following table. The percentage lost is simply the loss in kinetic energy (the change in kinetic energy) divided by the total initial kinetic energy.
    
    

    Collision #	total initial kinetic energy (J)	total final kinetic energy (J)	% loss in kinetic energy	e
    1
    2
    3
    4
    5

    
    
11. Look at the table you just filled out. For each collision, you determined what percentage of total kinetic energy was lost during the collision. How does this number compare to the value of e? What is the relationship between percentage loss in kinetic energy and e?

In the previous question, you should have seen that as loss in kinetic energy increases, e becomes smaller and smaller. e is a measure of how much kinetic energy is lost during a collision - it is an indicator of the elasticity of the collision. By definition, e is the coefficient of restitution and is the ratio of the final velocities to the initial velocities of the colliding objects:

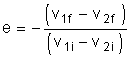
The value of e ranges from 1.0 to 0. For a perfectly elastic collision, e has a value of 1.0. For a perfectly inelastic collision, e has a value of 0.

12. Agree or disagree with the following statement: In a perfectly inelastic collision (e = 0), all kinetic energy is lost and the total final kinetic energy is 0. Support your answer with examples.
    
    
    
    
13. Prove that e must be 0 for a perfectly inelastic collision.
    
    
    

Analysing Collisions

We have now looked at two aspects of collisions: conservation of momentum and elasticity. We saw that in any collisions, momentum is always conserved (as long as there are no external forces acting on the system). Kinetic energy, however, is not always conserved - the elasticity of the collision is our clue to how much kinetic energy is conserved. These two pieces of information about a collision provides us with greater ability to analyse collisions and predict their outcomes.

In this section you will use both sets of equations to solve questions about collisions. These questions require several steps, but if you work carefully and follow a systematic approach (like the four-step method), they are easy to solve. For every question, use the applet to help you visualise the question and check you answer. Let's do an example together first

Example:

Object 1, with a mass of 3.0 kg, is travelling to the right at 6.1 m/s. It collides with object 2 which is at rest and has a mass of 8.0 kg. If e = 0.95, what is the final velocity of each object?

Solution:

1. Plan-it: Initially, only m₁ is moving and the total initial momentum is directed to the right. During the collision, m₁ hits m₂ and pushes it into motion - m₂ will move to the right. But what happens to m₁? This collision is almost elastic (e = 0.95) and since m₂ is much more massive than m₁, we can expect that m₁ bounces off m₂ and moves to the left. Playing the applet confirms this prediction.
   
   
2. Set-it-Up: First of all, let's list all the known and unknown information:
   
   We have two unknowns that we must solve for: v_1f and v_2f. But we also have two sets of equations: the law of conservation of momentum and our elasticity condition:
   
   
   Now, we substitute equation 2 into equation 1 to develop an expression for v_2f:
   
   
   
3. Solve-it: Now, we can substitute known values into equation 3 and solve for v_2f:
   
   Now that we know v_2f, we can substitute this value into equation 2 and solve for v_1f:
   
   After the collision, object 1 moves to the left at 2.6 m/s and object 2 moves to the right at 3.2 m/s.
   
   
4. Think-About-it: Our answer is verified with the applet. Furthermore, our answer matches our prediction.
   
   

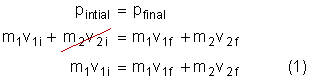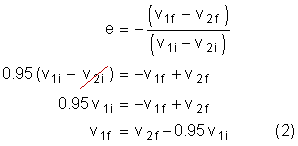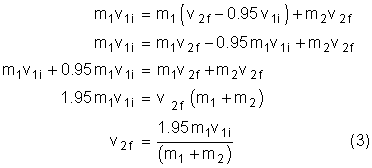
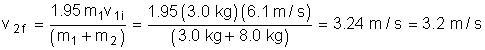
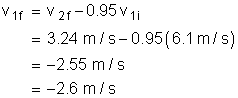
Now, it is your turn! For each question, assume that the collisions are head-on and that the system is a closed, isolated system.

14. Object 1, with a mass of 12.0 kg, is travelling to the right at 6.0 m/s. It collides with object 2 which is at rest and has a mass of 3.5 kg. If the collision is perfectly elastic, what is the final velocity of each object?
    
    
    
    
    
    
    
    
    
15. In a collision where e = 0.25, object A (mass = 5.0 kg ) collides with object B (mass = 5.0 kg). If object A was initially travelling to the right at 10.0 m/s and object B was at rest, what is the final velocity of each object?
    
    
    
    
    
    
    
    
    
16. Two objects, both with a mass of 7.0 kg, collide in a partially inelastic collision, where e=0.8. Initially, object 1 was moving to the right at 3.2 m/s and object 2 was at rest. After the collision, what is the final velocity of each object?
    
    
    
    
    
    
    
    
    
17. Object 1 (mass = 2.0 kg) is moving to the right at 9.23 m/s. It collides with object 2 (mass = 9.0 kg) which is at rest. If e = 0.78, what is the final velocity of each object?
    
    
    
    
    
    
    

Summary

In this lesson you looked at the total kinetic energy of a system before and after a collision. You discovered that kinetic energy is not always conserved in a collision. The key points covered in this lesson are:

• Kinetic energy is "energy of motion". Every object that is moving has kinetic energy:
  
• In a collision, the total kinetic energy of the system is not necessarily conserved. Kinetic energy can be converted to other forms of energy, resulting in a loss of kinetic energy.
• Whenever an object is distorted in a collision, there is a loss of kinetic energy.
• The elasticity of a collision is a measure of how much kinetic energy is conserved.
• The coefficient of restitution, e, is calculated by:
  
  
  • e = 1 - perfectly elastic collision (all kinetic energy is conserved)
  • 0 < e < 1 - inelastic collision (some kinetic energy is converted to other forms)
  • e = 0 - perfectly inelastic collision (objects stick together)
    
    
• Using both the conservation of momentum and the elasticity condition of a collisions allows us to analyse collisions when there are two unknowns.