Lesson 1 - Conservation of Momentum

The Collisions 1D applet simulates elastic and inelastic one-dimensional collisions in both the lab and centre of mass frames.

Prerequisites

Students should have a basic understanding of motion, velocity, vectors and equation manipulation.

Learning Outcomes

In this lesson you will learn about momentum and one dimensional collisions. Students will be able to define and calculate the momentum of an object. Students will also be able to qualitatively explain and quantitatively show that momentum is conserved in 1D collisions. As well, students will be able to approximate the results of a collision using conservation laws.

Instructions

Students should know how the applet functions, as described in Help and ShowMe. The applet should be open. The step-by-step instructions on this page are to be done in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited.

Contents

Background

In physics, there are two important kinds of quantities: vectors and scalars. You should already know the difference between the two. Understanding vectors is important when you study momentum. As review, answer the following questions.

  1. What is a scalar? Give two examples.

  2. What is a vector? Give two examples.

  3. Two soccer players are running toward each other, each with a speed of 10.0 km/hr. Do they have the same velocity? Why or why not?

In your study of momentum and collisions, you must also be aware of systems. A system is a collection of two or more objects and there are different types of systems that you must know about:

In this lessons when we examine the momentum of a system, it is important that the system under investigation is a closed, isolated system. It is easy to tell if a system is closed. However, it is a bit more difficult to determine if a system is isolated - you must be aware of any external forces that may be acting on the system.

  1. For the following questions, you are told what comprises the system. State whether or not the system is isolated. If the system is not isolated, identify the external force that is acting upon the system.
    1. Two basketballs (the system) are moving vertically in the air. One of the balls is falling down, while the other has just been thrown upward. The two balls run into each other as they move.


    2. Two cars (the system) are skidding along a gravel road and end up colliding with each other.


    3. Two skaters (the system) are coasting along frictionless ice and are headed straight for each other. They end up crashing into each other.


What is Momentum?

We use the word "momentum" in our everyday language to describe various events, such as sporting events, political campaigns or economic trends. However, regardless of what is being described, the word "momentum" always implies movement or the impetus for motion. For example, when we say, "the underdogs have gained the momentum", we mean that that team is "on the move" and will be difficult to stop - the greater the momentum, the harder it is to stop the team.

In physics, momentum has a similar meaning. Simply put, momentum is "mass in motion", or a measure of how much motion an object has. Algebraically, momentum is defined as the product of an object's mass and velocity, . Since velocity is a vector, so too is momentum. The direction of the momentum vector is in the same direction as the velocity.

Momentum

Momentum is "mass in motion". Every object that is moving has momentum. Momentum is a vector and is in the same direction as the velocity.
  1. Calculate the momentum of:
    1. a 10.0 kg bird that is flying 8.0 m/s east.

    2. a 70.0 kg object travelling west at 5.0 m/s.

    3. a 500.0 kg truck that is at rest.

    4. a 200 kg car travelling 100 km/hr west.


  2. Which of the following have a greater magnitude of momentum?
    1. a 500.0 kg truck travelling at 60 km/hr or a 200.0 kg car travelling at 60 km/hr?

    2. a 15.0 kg object travelling to the right at 5.0 m/s or a 15.0 kg object travelling to the left at 5.0 m/s?

    3. a 500.0 kg truck travelling at 60 km/hr or a 200 kg car travelling at 150 km/hr?

    4. a 500.0 kg truck at rest or a 200 kg car at rest?

    5. a 200 kg truck at rest or a mosquito flying at 2 m/s?


Conservation of Momentum

Any object that is moving has velocity, and also momentum. But what happens if two or more objects collide? What happens to the velocity or the momentum of each object? Let's explore this question with the applet. For the following questions, un-check Show CM and Show CM Frame.

  1. Using the applet, perform five different collisions and complete the following tables. To generate a new collision, either set your own conditions or press the new button ( ). To view the collision information, press the data button ( ).

    Collision 1
    Object
    mass
    (kg)
    vinitial
    (m/s)
    vfinal
    (m/s)
    D v
    (m/s)
    pinitial
    (kg·m/s)
    pfinal
    (kg·m/s)
    D p
    (kg·m/s)
    Blue
     
     
     
     
     
     
     
    Green
     
     
     
     
     
     
     

    Collision 2
    Object
    mass
    (kg)
    vinitial
    (m/s)
    vfinal
    (m/s)
    D v
    (m/s)
    pinitial
    (kg·m/s)
    pfinal
    (kg·m/s)
    D p
    (kg·m/s)
    Blue
     
     
     
     
     
     
     
    Green
     
     
     
     
     
     
     

    Collision 3
    Object
    mass
    (kg)
    vinitial
    (m/s)
    vfinal
    (m/s)
    D v
    (m/s)
    pinitial
    (kg·m/s)
    pfinal
    (kg·m/s)
    D p
    (kg·m/s)
    Blue
     
     
     
     
     
     
     
    Green
     
     
     
     
     
     
     

    Collision 4
    Object
    mass
    (kg)
    vinitial
    (m/s)
    vfinal
    (m/s)
    D v
    (m/s)
    pinitial
    (kg·m/s)
    pfinal
    (kg·m/s)
    D p
    (kg·m/s)
    Blue
     
     
     
     
     
     
     
    Green
     
     
     
     
     
     
     

    Collision 5
    Object
    mass
    (kg)
    vinitial
    (m/s)
    vfinal
    (m/s)
    D v
    (m/s)
    pinitial
    (kg·m/s)
    pfinal
    (kg·m/s)
    D p
    (kg·m/s)
    Blue
     
     
     
     
     
     
     
    Green
     
     
     
     
     
     
     


  2. Now, look at the information you recorded and calculated in the previous question. Can you see any interesting relationships between what happens to the blue mass and the green mass?
    1. Is there a relationship between the change in velocity of the blue mass and the green mass? If yes, describe the relationship.




    2. Is there any connection between the change in momentum of the blue mass and the green mass? If yes, describe the relationship.



You should see an interesting connection between the change in momentum of each mass: the changes in momentum should be equal, but opposite. For example, if the blue mass has an increase in momentum, than the green mass has a decrease in momentum, by the same amount. This connection leads us to an important concept about momentum and what happens to the total momentum of a system in a collision. Let's explore this idea a little more.

  1. If the change in momentum of one object is exactly equal, but opposite to the change in momentum of another object, what does that indicate about the total momentum of the system?




  2. If the total momentum of a system before a collision is equal to the total momentum of a system after a collision, then we say that momentum is conserved. For the five collisions you performed earlier, check that momentum is conserved:

    Collision # total initial momentum

    (kg·m/s)    		 total final momentum

    (kg·m/s)    		 Is momentum conserved?
    1      
    2      
    3      
    4      
    5      

  3. You have discovered that within a closed and isolate system, the change in momentum of one object is equal and opposite to the change in momentum of another object. You have also seen that the total momentum of a closed and isolated system is conserved in a collision. Now, starting with your discovery that the change in momentum of one object is equal and opposite to the change of another () algebraically derive the conservation of momentum.






You have just discovered one of the most important laws in physics - the Law of Conservation of Momentum. This law governs all physical interactions - it is considered to be one of the fundamental laws of physics. The law of conservation of momentum has been used to investigate and analyse all types of interactions, from the subatomic world of electrons, protons and even smaller things, all the way up to the astronomical world of planets, stars and galaxies. This law is one of the key laws that governs the way our world works.

The Law of Conservation of Momentum

For any closed, isolated system, the total momentum does not change. In a collision, momentum is conserved - the total momentum before the collision is equal to the total momentum after the collision.

In a collision, the total momentum of a system is conserved, as long as no external forces act on the system. There are, however, different types of collisions - sometimes objects bounce off each other, while other times, the objects stick together. In an elastic collision the total kinetic energy of the system is conserved. In an completely inelastic collision the objects stick together upon impact and travel as one whole unit after the collision. You will learn about the differences between these types of collisions in another lesson.

Analysing Collisions

In the previous section you discovered that the total momentum of a system is conserved, as long as there are no external forces acting on a system. Let's use the conservation of momentum to analyse the following collisions. When solving multi-step questions, it is useful to follow a four-step method:

Let's do an example question together:

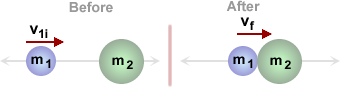
Example:

A 2.0 kg mass, moving to the right at 2.97 m/s collides inelastically with a 10.0 kg mass that is at rest. If the objects stick together, what is the velocity of the system after the collision?

Solution:

  1. Plan-it: Initially, m1 moves to the right and m2 is at rest. After the collision, the objects stick together and move as one great big mass (m1+m2). Since the total initial momentum is directed to the right, the total final momentum must also be directed to the right. Since the objects stick together, they both move to the right.

  2. Set-it-up: Motion to the right is positive. Our unknown information is the final velocity of the system, vf.

    We will use the Law of Conservation of Momentum to solve this question. We need to solve for vf:


  3. Solve-it: Now, we simply substitute in the known values and calculate vf:

    After the collision, the system moves to the right at 0.50 m/s.

  4. Think-About-it: We predicted that the system would move to the right - our answer agrees with our prediction. You can also run this scenario on the applet to check the answer (set e=0).

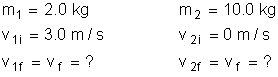
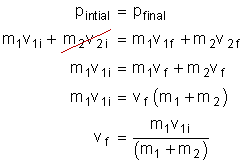
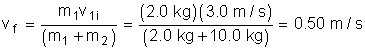
Now it's your turn! For all questions, assume that the objects collide head-on and the system is a closed, isolated system.

  1. A 5.0 kg object is travelling to the right at 10.0 m/s. It hits a 7.0 kg that is initially at rest. After the collision, the 5.0 kg continues to move to the right, but now at 1.17 m/s. In what direction and with what speed is the other object moving?





  2. A 10.0 kg object has collided in a completely inelastic collision with a 2.0 kg object that was initially at rest. After the collision, the system moves to the right at 2.56 m/s. What was the initial velocity of 10.0 kg object?





  3. Object A, with a mass of 2.0 kg, is travelling to the right at 15.0 m/s. Object B, with a mass of 12.5 kg, is travelling to the left, also at 15.0 m/s. If the two objects stick together upon impact, what is the final velocity of the system?





  4. When you shoot a gun, it "kicks back", or recoils.
    1. Using conservation of momentum, explain why a gun recoils when you shoot it.


    2. If a 30 g bullet is shot from a 7.5 kg gun, and has a velocity of 300 m/s, what is the recoil velocity of the gun?





  5. A 250 g firecracker explodes into two pieces. The first piece, 97 g, flies off to the right at 16 m/s. What is the velocity of the second piece?





  6. Are the following collisions possible? Why or why not?
    1. An object, with mass m, initially travelling to the right collides inelastically with another object, also mass m, that is at rest. After the collision the system moves together to the left.



    2. An object, A, initially travelling to the right collides with another object, B, that is at rest. After the collision, A moves back to the left and B remains at rest.



    3. An object, A, initially travelling to the right collides with another object, B, that is at rest. Object B is more massive than object A. After the collision, A moves back to the left and B moves to the right.



    4. An object is travelling to the right and collides with another object that is at rest. After the collision, both object travel to the right, but at different speeds.

 

Summary

In this lesson, you investigated the momentum of a closed, isolated system during a collision. You have discovered one of the fundamental laws that governs physical processes: the Law of Conservation of Momentum. The key points you learned in this lesson are: