Lesson - Atwood's Pulley

The applet Atwood simulates the motion of two masses connected by a massless, ideal string which passes over a massless pulley.

Preamble

This lesson will give you practice using the concepts of energy conservation and energy transformation.

The applet should be open. The step-by-step instructions in this lesson are to be carried out in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited. You should be prepared to do calculations to verify the numbers that are generated by the applet.

Contents

Please answer the following questions in the space provided.

Potential Energy and defining a zero-point for Potential Energy

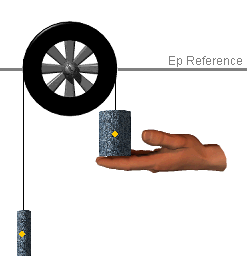
In order to assign a numerical value to the potential energy of a body it is first necessary to define a "zero point" or reference level at which the potential energy is considered to be 0 J. You do this on the applet by repositioning the Ep Reference line by moving it up or down. To see how this works, position the Ep Reference line to be at the same height as the center of the pulley as shown on the right. Set mass 1 to equal 250 g and mass 2 to be 750 g.

  1. Are the initial potential energies for mass 1 and mass 2 positive, negative or zero in this case? Explain your answer.

 

 

  1. Run the applet (press ), and produce a graph showing the potential energy for each mass as a function of time. Explain why the graphs look the way they do.

 

 
  1. Mass 1 climbs by 1.133 m and mass 2 drops by 1.133 m. Calculate the change in potential energy for each mass. Recall that , where DEp is the change in potential energy, m is the mass, g = acceleration of gravity and Dh is the change in height. Show how the change in energy for each mass can be measured from the graphs that you produced in question 2.






  2. Its clear that we didn't pick the most convenient place for the Ep Reference line. Reset the applet (press ) and this time put the Ep Reference line through the yellow dot which represents the center of mass for mass1. When released, mass 1 will move above this line and its Ep will increase. Since mass 2 is already above this line and it drops, its Ep will start at its maximum value and then decrease. Calculate the initial potential energy for mass 2 relative to this new Ep Reference line and use the applet to verify your calculation (hint: redo the graphs that you created in question 2). What is the initial potential energy for mass 2?





  3. Combine the initial potential energy for each mass (Ep1 + Ep2). This represents the initial potential energy for the system. What is this energy. Run the applet. Now, what is the potential energy of the system? Are these two energies the same?

 

Calculating Potential and Kinetic Energy

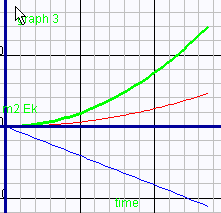
In the previous example the initial potential energy of the system was greater than the final potential energy (by about 5.56 J). What happened to this energy?

Answer: When you press play, the masses begin to accelerate. Mass 1 moves up, mass 2 moves down. A new energy form, kinetic energy, is now being created. Recall, kinetic energy is given by the expression , where m is the mass and v is the velocity.
  1. Re-run the applet using the same mass values used in the previous section. Produce kinetic energy - time graphs for each mass and a graph showing velocity-time (the velocity will be the velocity for mass 2 - mass 1's velocity is just the negative of this). Your graph should look something like the one shown on the right. How fast is each mass moving at t = 0.50 s? What is the kinetic energy for each mass at this time? Answer this by calculating the kinetic energy and then verify this result by inspecting the graph. (Tip: use the "drag-and-zoom" button to zoom-in on points of interest on the graph. Alternately, generate a data table and look up the velocity and energy at t = 0.50 s.)







  2. The total energy of the system is just the sum of all the kinetic and potential energy terms at any instant. Find the total energy of this system at t = 0.00s, t = 0.50 s and t = 0.68 s. What do you notice about these three number?

 

Total Mechanical Energy of a System and Conservation of Energy

The applet Atwood assumes that there is no loss of energy from the system. This means that there is no frictional loss in the pulley and that air resistance on the moving masses can be ignored. It is assumed that energy is conserved. When this happens we can conclude that the total energy of the system is constant. This can expressed in the following ways:

 The net change in energy in the system is zero. Energy is neither lost or created
The total energy of the system before is equal to total energy of the system after any motion or change.
The individual expressions for the energy can change but their sum must be zero. Increases in one term will be offset by decreases in other terms.

These are just three ways of stating the Principle of Conservation of Mechanical Energy.

  1. Set up the applet so that mass 1 = 200 g and mass 2 = 800 g. Please fill out the following table and verify the results by using the applet Atwood:
System
Before Masses Released
Masses Released and mass one has moved up 0.5 m
Ep1(J)
    
Ep2(J)
    
Ek1(J)
    
Ek2(J)
    
E total (J)