lesson_atwood

The applet should be open. The step-by-step instructions in this lesson are to be carried out in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited. You should be prepared to do calculations to verify the numbers that are generated by the applet.

What is a Free Body Diagram?

Free Body Diagrams are an indispensable tool used in the analysis of forces and the application of Newton's Laws. Essentially, a Free Body Diagram is a representation of all forces acting on a body. If a system consists of more than one body then it is essential that a free body diagram be constructed for each object. In what follows you should use the applet Free Body Drawer to help give you practice in creating Free Body Diagrams. As you will see, with a little practice and careful attention to details, making a Free Body Diagram is an easy process that will greatly improve you ability to understand otherwise complex physical situations.

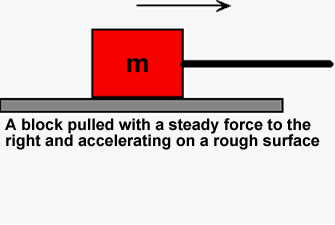
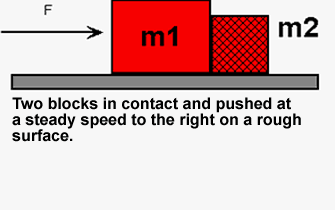
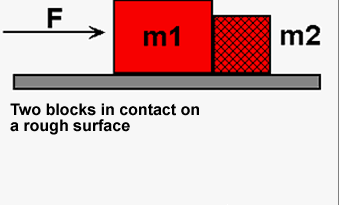
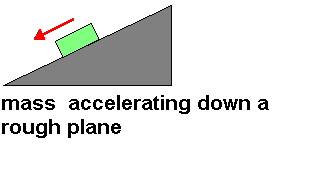
How to Draw Free Body Diagrams

Press the projects button in the upper left () and select the project labeled "project". Load the image shown on the right. A correct Free Body Diagram for this situation would show 4 forces: the gravitational force or weight of the block the Normal force of the surface pressing up on the block the frictional force opposing the motion of the block the force applied by the rope and directed to the right Use the applet to draw in theses forces and then compare your drawing with the computer generated FBD.
Let's look carefully at the FBD for this example. Your FBD should look similar to the one appearing on the right. A common practice (but not essential) is to draw the FBD away from the original diagram and just as a set of vectors emerging from a point. In this example you can see the 4 forces identified in part 1. Since the surface is level the Normal force and the Weight are equal and acting in opposite directions. Similarly, the block is not accelerating to the right. This tells us that the net force to the right is zero and that the frictional force is equal in magnitude and opposite in direction to the Tension force applied by the rope.
As a slightly different version of the previous example, try the setup shown at the right: which is part of the FBD's in this project:. Identify the 4 forces relevant to this FBD and draw the FBD. Make sure to explain why you drew the forces the way you did.

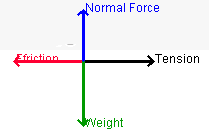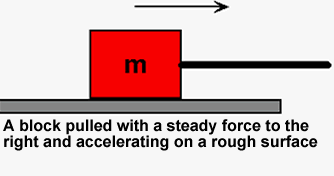How to Create Equations from Free Body Diagrams

Let's make a FBD for the system shown on the right. Now we see two bodies in the system and hence must make two FBD's. The FBD for m1 will be identical to the one you made in the previous example. The FBD for m2 will show the combination of two forces: Weight and Tension. The FBD's are shown below. As well, note that a set of coordinate axes have been drawn in. YOU MUST CHOOSE THIS - the applet will not assign coordinates or draw them in.
	Choosing Coordinate Axes is essential if you are to assign correctly the directions (hence signs) for forces. Any force pointing in the +X or +Y directions will be treated as positive and ay force in the opposite directions will be treated as negative. We are now able to write simple equations describing the forces in the X and Y directions for each body. This is done below:
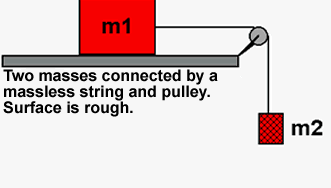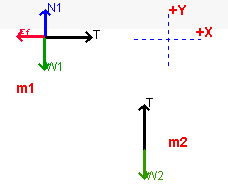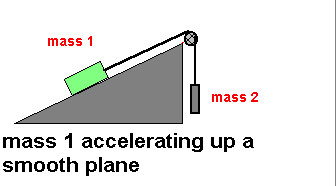
Equations for Mass 1	In the X direction: Tension points in the positive direction while Force of friction is in the negative direction. This becomes . But the net force, by Newton's Second Law is always , so the X-equation becomes In the Y direction: the Normal force points up (positive) and Weight is down (negative) and the mass is not accelerating in this direction (net force is zero) so .
Equations for Mass 2	In the Y direction: the Tension force acts upward (positive) while the weight force acts downward. Also, mass 2 is accelerating in the downward direction. The equation for mass 2 is: