Prerequisites
For the section on units, students should be familiar with the units of basic physical quantities. For the sections on Kepler's laws, no special physics background is required. For the concluding section on some of the underlying physics and on the special unit system used in the Lesson, students should be familiar with the concepts of force, acceleration, speed, angular speed and the radian measure of angles, and be familiar with Newton's second law, Newton's law of universal gravitation, and acceleration in uniform circular motion.
Learning Outcomes
Students will develop an understanding of Kepler's three laws of planetary motion and will deepen their understanding of some of the related dynamics and kinematics.
Instructions
Students should know how the applet functions, as described in Help and ShowMe.
The applet should be open. The step-by-step instructions in the following text are to be done in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited.
![]() Kepler's Three Laws of Planetary
Motion
Kepler's Three Laws of Planetary
Motion
![]() Some Kinematics and Dynamics Related
to Kepler's Laws
Some Kinematics and Dynamics Related
to Kepler's Laws
![]() Kepler's Three Laws for the Case of
Uniform Circular Motion
Kepler's Three Laws for the Case of
Uniform Circular Motion
![]() Appendix
Appendix
![]() Definitions of Radian Measure of
Angle, Angular Speed, Areal Speed
Definitions of Radian Measure of
Angle, Angular Speed, Areal Speed
![]() Derivation of Expression for Areal
Speed
Derivation of Expression for Areal
Speed
Exercise 1. Display the data box by clicking the Data
button  . Its contents are illustrated in Figure 1 below (but
most likely with values different from those in your case).
. Its contents are illustrated in Figure 1 below (but
most likely with values different from those in your case).
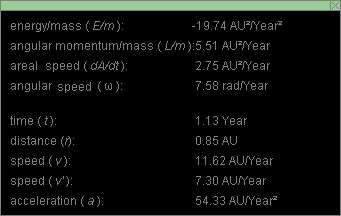
Figure 1
Observe that the various quantities are displayed in units involving the units "AU" and "Year". These are convenient units in an astronomical context.
The AU is the astronomical unit. It is a unit of distance and is equal to the semi-major axis of the earth's orbit around the sun. 1 AU = 1.496×1011 m.
The Year is the time it takes the earth to make one revolution around the sun relative to the fixed stars. This is also called the the sidereal year. 1 Year = 365.26 mean solar days. The sidereal year must be distinguished from the calendar year which is equal to 365 or 366 mean solar days, depending on the particular year. It must also be distinguished from the tropical year and the anomalistic year which do not concern us in this applet.
Exercise 2. Make a dimensional analysis of all quantities listed in Figure 1, and determine if the units shown are dimensionally correct. E.g., speed has the dimensions of length/time. This is consistent with the unit AU/Year displayed for speed in Figure 1.
Johannes Kepler (1571-1630) worked out three laws of planetary motion. These laws describe the manner in which the planets move around the sun. They do not explain why the planets move in this fashion. That explanation was provided later by Isaac Newton (1642-1727).
Kepler's three laws were based on observations by Tycho Brahe (1546-1601). They amounted to a great simplification and increased accuracy in the description of the planets' motions compared to the earlier Copernican model. This advance was brought about when Kepler realized that planets were moving in elliptical orbits, rather than on epicycles of circles as in the Copernican model.
Kepler's laws are now known to be true only to an approximation, but a very good one. The observed deviations of the planets' motions from Kepler's laws can for the most part be explained in terms of Newton's laws of motion applied to the planets in combination with his universal law of gravitation.
The Newtonian analysis shows that Kepler's laws would be true exactly if the gravitational force exerted on the planets by the sun were the only force acting on the planets. However, the planets also exert gravitational forces on each other, and it is these additional small forces that cause the planets' motions to be slightly different from those predicted by Kepler's laws.
Newton's theory can explain these deviations from Kepler's laws, except for one remaining small discrepancy which was accounted for early in the twentieth century by Einstein's theory of general relativity.
Exercise 1. RESET the applet.
Set the eccentricity ε and the semi-major axis a to
ε = 0.400 ![]() and
and
![]() a = 2.0 AU,
a = 2.0 AU, ![]() (1)
(1)
respectively. PLAY the motion.
Question 1. Just eye-balling the way the planet (green) is moving around the sun (yellow), how would you describe the shape of the orbit and the location of the sun relative to the orbit?
Based on the most precise observations available at the time, made by the astronomer Tycho Brahe, Kepler described the orbits of all planets in his first law.
Kepler's first law. The orbit of a planet around the sun is an ellipse, with the sun located at one of the two focal points of the ellipse.
Comment 1. An ellipse is a curve such that for any point P on this curve the sum of the distances r1 and r2 from P to two fixed points F1 and F2 is constant. The fixed points F1 and F2 are called the focal points of the ellipse. The sum of the two distances r1 and r2 obeys the equation
r1 + r2 = 2a
![]() (2)
(2)
where 2a is the length of the major axis of the ellipse, the longest diameter of the ellipse. Figure 2 below illustrates these quantities.
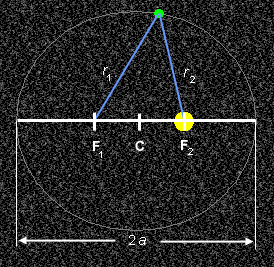
Figure 2
Exercise 1. Continuing from the previous section,
REWIND the applet. Display the sectors of equal area by
clicking the Area Sweep button  .
.
Using the time values from the data box, measure the times required for the planet to traverse several of these sectors of equal area, one sector at a time. What do you observe?
Answer. Kepler, based on Brahe's observations, provided an answer to this question in his second law.
Kepler's second law. In equal time intervals, the radius vector from the sun to a planet sweeps across equal areas.
Comment 1. One can also state this law by saying that a planet's areal speed is constant. Areal speed is defined as the limit of the ratio DA/Dt as Dt goes to zero. Here DA is the area swept over by the radius vector from the sun to the planet during the time interval Dt. We'll use the symbol dA/dt for areal speed.
Comment 2. Most books use the term "areal velocity" rather than "areal speed" to refer to dA/dt. For consistency's sake, since dA/dt is a positive scalar quantity, not a vector, let's call it "areal speed".
Exercise 1. Continuing from the previous section, hide the sectors of equal area. Measure the period of the planet. Repeat this for another orbit with the same semi-major axis, but different eccentricity. Repeat this for yet another orbit with different semi-major axis, and again for a fourth orbit with the same semi-major axis as the last one but different eccentricity.
Thus, measure the period for two pairs of orbits. The orbits of each pair have the same semi-major axis but different eccentricity. Based on your observations, answer the following questions.
Question 1. How does varying the eccentricity affect the period?
Question 2. For each orbit, what is the value of the ratio T2/a3 where T is the period?
Kepler, based on Brahe's observations, answered these questions in his third law.
For all planet orbits, the square of the period is proportional to the cube of the semi-major axis.
Comment 1. In the units of AU and Year that we are using, the proportionality constant is numerically equal to 1, i.e., if T is in Year and a in AU, then numerically the following equation holds:
T2 = a3, ![]() where
a is in AU and T in Year .
where
a is in AU and T in Year . ![]() (3)
(3)
Exercise 2. The semi-major axis of the orbit of Mars is 1.52 AU. Calculate the period of Mars in Year.
Exercise 1. RESET the applet. Set the eccentricity and semi-major axis to the same values as in the earlier Equation (1),
ε = 0.400 ![]() and
and
![]() a = 2.0 AU.
a = 2.0 AU. ![]() (1')
(1')
PLAY the motion, and observe how the radius vector sweeps through a larger angle in a given time interval when the planet is closer to the sun than when it is farther away from the sun.
Exercise 2. REWIND the applet, and display the angular-speed graph. PLAY the motion again. Does the graph have a maximum when the planet is closest to the sun and a minimum when the planet is farthest from the sun?
Exercise 3. Measure the period T of the planet, and then determine the areal speed by dividing the area A of the ellipse by T. Since the areal speed is constant, one can determine its constant value this way. When done, compare your value to that shown in the applet's data table.
To determine the area of the ellipse, use the following equation
A = πab
![]() (4)
(4)
where b is the semi-minor axis. The minor axis is the axis perpendicular to the major axis. The semi-minor axis is given by the expression
b = a (1 - ε2)1/2 .
![]() (5)
(5)
The geometry that defines b and underlies Equation (5) is illustrated in Figure 3 below.
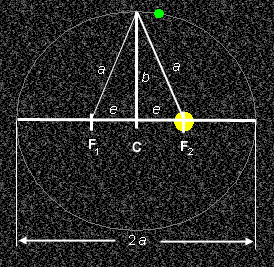
Figure 3
To understand Equation (5), look at the right-angle triangle formed by the sides b, a, and e and containing the sun in the right-hand corner. Applying the Pythagorean theorem to this triangle gives
a2 = b2 +
e2 ![]() (6)
(6)
whence
b2 = a2 -
e2. ![]() (7)
(7)
From the definition of the eccentricity, ε = e/a, it follows that
e = ε a
.![]() (8)
(8)
Substituting this expression into Equation (7) gives
b2 = a2 -
ε2
a2 = a2(1 -
ε2). ![]() (9)
(9)
Taking the square root of both sides of Equation (9) gives Expression (5) for b.
Let's now have a look at how the areal speed dA/dt is related to the angular speed ω and the radius r.
Exercise 4. The areal speed dA/dt can depend on only these two dimensional quantities: the radius r from the sun to the planet and the angular speed ω (Greek letter; read: omega) with which this radius sweeps over the orbital area. Clearly, the larger r is the more area will be swept over in a given amount of time and the larger ω is the more area will be swept over in a given amount of time. With this in mind, one can imagine a number of ways in which dA/dt could depend on r and ω. E.g., dA/dt might be equal to
where c is a dimensionless quantity that could still vary from point to point along the orbit.
Make a dimensional analysis to determine which combination of powers of r and ω is the only possibility in the expression for dA/dt. Note that the dimensions of w are 1/time because the radian measure of an angle can be treated as a dimensionless number.
Exercise 5. The combination r2ω is the only one that has the same dimension as dA/dt. Now investigate whether the factor c in front of r2ω is a constant.
Do this by evaluating the product r2ω at three or more points along the orbit and check if it is constant. Values of r and ω are displayed in the applet's data box.
If you find r2ω to be a constant, evaluate c by using the value of dA/dt from Exercise 3. Therefore, what is dA/dt equal to in terms of r and ω?
Exercise 6. Derive a theoretical expression for dA/dt in terms of r and ω for the special case of uniform circular motion.
Hint. The area A of a circle of radius r is given by Equation (4) with b = a = r. Thus, A = πr2. The angular speed ω is equal to the angle corresponding to a full circle, which is 2π rad, divided by the period T.
Comment. The expression for dA/dt in terms of r and ω for a general motion is derived in the section Derivation of Expression for Areal Speed of the Appendix.
Exercise 7. For the settings defined in Equation (1') above and your value for the areal speed obtained in Exercise 3, do the following calculations. Use the general expression (A6) for dA/dt derived in the Appendix to calculate the planet's angular speed when the planet is closest to the sun (perihelion), farthest from the sun (aphelion), and at the top of the orbit where the minor axis intersects the ellipse. Compare your answers to those provided by the applet.
Hint. To determine the distances sun-planet in the three positions, refer to Figure 3 above. To evaluate e in terms of the eccentricity and semi-major axis, use Equation (8) above.
ε = 0.400 ![]() and
and
![]() a = 1.0 AU.
a = 1.0 AU. ![]() (10)
(10)
Display the planet's acceleration vector. PLAY the motion, and observe how the acceleration vector changes. Describe in words how the direction and magnitude of the acceleration vary while the planet makes one revolution around the sun.
Exercise 2. Determine the dependence of the magnitude a of the acceleration (not to be confused with the semi-major axis a) of the planet on the distance r from the sun to the planet. Display the applet data, and get values for a and r at three or more points along the orbit.
Repeat this for at least two more orbits, with different eccentricities and/or semi-major axes. For each orbit, find an equation that gives a in terms of r. Then predict what the corresponding equation will be for yet another orbit and check your prediction.
Hint. Evaluate the product ar2 for every point at which you observe a and r. (Again, here a denotes the magnitude of the acceleration.)
Question 1. The acceleration that you observe is caused by the gravitational force exerted by the sun on the planet. Are your observations consistent with this statement? If so, why?
Hint. Think of what you know about the magnitude and direction of this force.
Answer. The only force acting on the planet is the force exerted on it by the sun. This is true at least in the applet, because there are no other objects around that could be interacting with the planet. (In reality, other planets also exert forces on a given planet, but these forces are a lot weaker than the force exerted by the sun.) According to Newton's law of universal gravitation, the force exerted by the sun on the planet is directed towards the sun and has magnitude
Fgrav =
GMm/r2. ![]() (11)
(11)
Here G is the universal gravitational constant, which has the value
G = 6.67×10-11 N m2
kg-2. ![]() (12)
(12)
M is the mass of the sun and m the mass of the planet.
Newton's second law of motion applied to the planet gives the equation
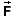 grav = m
grav = m 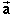 .
.![]() (13)
(13)
This equation implies that the planet's acceleration is in the same direction as the force exerted on the planet by the sun, which is towards the sun at all times.
Equation (13) and Equation (11) combined imply that the magnitude of the acceleration is equal to
a = GM/r2.![]() (14)
(14)
Equation (14) says that the magnitude of the planet's acceleration is inversely proportional to r2 and that the proportionality constant, GM, does not depend on what the orbit is and what planet it is, because the planet's mass m does not enter into this constant. You should have been able to observe these facts when doing Exercise 2.
Question 2. Is the equation a = v2/r true for the magnitude a of a planet's acceleration at any point of the planet's orbit, where v is the planet's speed at that point? When would you expect this equation to be true? Test your prediction with the applet.
For the case of circular orbits, the derivation of Kepler's three laws is not difficult and does not need calculus. Let's go through the derivation for circular orbits.
Kepler's First Law. What needs to be shown is that a planet can revolve around the sun in a circular orbit with the sun at the center of the orbit. (The two focal points coincide with the center of the circle when the eccentricity is zero.)
The argument begins with Newton's second law applied to the planet, as in Equation (13) above. Suppose a circular orbit of radius r is possible and that the planet moves in it with constant speed v. Then we know from the kinematics of uniform circular motion that the acceleration is directed towards the center of the circle. Thus, Equation (13) is satisfied as far as the directions of the vectors on both sides of the equation are concerned if the sun is at the center of the circle and the planet's speed is constant.
Equation (13) must be satisfied also with respect to the magnitudes of both sides of the equation. The magnitude of its left-hand side given by Expression (11). From the kinematics of uniform circular motion, we know that the magnitude of the acceleration is equal to
a = v2/r. ![]() (15)
(15)
Equation (13) can be satisfied if the speed v has the value worked out below. This proves that circular planetary motion is possible.
To find the speed v, take magnitudes of both sides of Equation (13), divide both sides by m, and use for a Expression (15). Then
GM/r2 =
v2/r. ![]() (16)
(16)
Solving this equation for v gives the speed a planet must have to keep moving in a circle of radius r around the sun.
Exercise 1. Approximate both the orbits of Earth and Mars by circular orbits of radii 1.0 AU and 1.5 AU, respectively. The speed of Earth is 2π AU/Year. What is the speed of Mars in astronomical units? You do not need to know the value of GM to work out the answer.
Exercise 2. From the data for Earth's orbit given in Exercise 1, determine the value of the constant GM in astronomical units.
Kepler's Second Law. We have seen that a planet can orbit the sun in a circle if the planet has the right speed and if the sun is at the center of the circle.
It is self-evident, that the areal speed will be constant in this case.
Kepler's Third Law. Kepler's third law follows from Equation (16) above if we substitute
v = 2πr/T![]() (17)
(17)
where T is the planet's period. 2πr is the circumference of the circle, which is the distance traveled by the planet during time T.
Substituting Expression (17) into Equation (16) gives
GM/r2 = (2πr/T)2/r
= (2π)2r/T2.
![]() (18)
(18)
This equation can be rewritten as
GM/(2π)2
× T2 = r3 .
![]() (19)
(19)
This is Kepler's third law for circular motion. The square of the period is proportional to the cube of the radius. The proportionality constant is the same for all possible orbits. It is determined by the mass of the sun, apart from the universal gravitational constant.
Although we have not proved Kepler's third law for elliptical orbits, the same proportionality constant GM/(2π)2 applies in all cases if r is replaced by the semi-major axis a. Thus, Kepler's third law for a general elliptical motion is
GM/(2π)2
× T2 = a3 .
![]() (20)
(20)
For Earth, a = 1 AU and T = 1 Year, by definition. These parameters must satisfy Kepler's third law as well. Thus,
GM/(2π)2
× 1 Year2 = 1 AU3 .
![]() (21)
(21)
Thus, the constant GM/(2π)2 is equal to
GM/(2π)2 = 1
AU3 Year -2 .![]() (22)
(22)
Comment 1. Equation (22) implies that, if we use the AU and the Year as length and time units, the numerical part of GM/(2π)2 must be equal to 1.
Exercise 3. Use either Equation (21) or (22) to work out the mass of the sun. Use 1 AU = 1.496×1011 m and 1 Year = 3.156×107 s. The value of the gravitational constant G in SI-units is given in Equation (12) above.
Comment 2. Substituting Expression (22) into Kepler's third law (20) shows that in units of AU and Year this law has the simple form
(1 AU3 Year -2) ×
T2 = a3 .
![]() (23)
(23)
If one is interested only in numerical values, one can write Equation (23) as
T2 = a3, ![]() where a in AU and T in Year .
where a in AU and T in Year .
![]() (24)
(24)
In this form, Kepler's third law was already stated in Equation (3) above.
>>>>> Appendix <<<<<
The quantities needed in the definitions of the quantities in the title of this section are listed below and are illustrated in Figure A1.
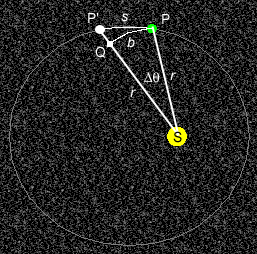
Figure A1
Definitions of symbols:
Δθ = b/r . ![]() (A1)
(A1)
Example: If b = 0.6 AU and r = 4.0 AU, then Δθ = 0.6/4.0 = 0.15 rad.
Note that angles in radians can be treated like dimensionless numbers in a dimensional analysis because their measure is the ratio of two dimensionally equal quantities, namely, the ratio of two lengths.
ωav =
Δθ/Δt . ![]() (A2)
(A2)
The angular speed at a given instant, ω, is the limit of the average angular speed as the size Δt of the time interval containing the given instant goes to zero.
It is customary when dealing with angular speed to measure angles in radians. The SI-unit of angular speed is rad/s.
(dA/dt)av = ΔA/Δt .
![]() (A3)
(A3)
The areal speed at a given instant, dA/dt, is the limit of the average areal speed as the size Δt of the time interval containing the given instant goes to zero.
The average speed during the time interval &Deltat, vav, is defined by the following ratio:
vav = s/Δt . ![]() (A4)
(A4)
The speed at a given instant, v, is the limit of the average speed as the size Δt of the time interval containing the given instant goes to zero.
All quantities involved in the expression, radius, angular speed, and areal speed, are relative to a reference point. In Figure A2 below, this point is point S, the location of the sun, but the reference point could be chosen anywhere else as well.

Figure A2
Derivation. The derivation is based on the geometry illustrated in Figure A2. The symbols in Figure A2 are explained following the identical earlier Figure A1. It will be assumed that you know the definitions of the radian measure of an angle, and of angular speed and areal speed as presented in the preceding section.
The area ΔA of the triangle SPP' can be approximated by the area of the triangle SPQ. (The word "triangle" is used here because the arcs PP' and PQ approach straight lines as Δt and Δθ go to zero.) In making this approximation, the area of the small triangle PP'Q is neglected. In the limit as Δt and Δθ go to zero, the error due to this approximation vanishes. Reason: in this limit, the area of triangle PP'Q becomes negligible in comparison to that of SPQ.
The length b of the base PQ of the triangle SPQ is equal to rΔθ if Δθ is in radians. This follows from Definition (A1) of the radian measure of angles.
As Δθ goes to zero, the base PQ approaches a straight line, and the triangle SPQ with curved base PQ approaches an isosceles triangle with a straight base. Also, the height of this triangle, extending from the midpoint of the base to point S, becomes indistinguishable from the side r.
The area of a triangle is equal to ½×base×height. Therefore, in the limit as Δθ goes to zero, we can evaluate the area of the triangle SPQ as ½×rΔθ×r. Thus, when approaching this limit, we can use
ΔA = ½
r2Δθ,
![]() for
for ![]() Δθ
Δθ 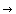 0.
0. ![]() (A5)
(A5)
Dividing both sides of Equation (A5) by Δθt, going to the limit, and writing dA/dt for ΔA/Δt and ω for Δθ/Δt, gives for the areal speed at point P
dA/dt = ½
r2ω .
![]() (A6)
(A6)
Nowhere in this derivation did we use the fact that the particle is moving in an ellipse. Therefore, Expression (A6) for the areal speed of a particle is valid for any curve and any motion along that curve. The point S in general is an arbitrary fixed reference point. The value of the areal speed at a given instant, as those of r and ω, will depend on the choice of point S, but the form of Relation (A6) will not.